2014-02-12
1061
Оригиналы с рациональными изображениями
1. Изображения степенных и показательных функций. При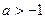 
степенная функция 
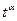является оригиналом с нулевым показателем поста, причем
,
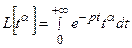что при положительных значениях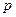 
равно (после замены 
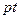на t)
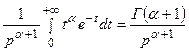(21.6)
Необходимо отметить, что в силу теоремы единственности, которая гласит: если в области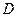 
даны две аналитические функции, совпадающие на множестве точек, имеющем хотя бы одну предельную точку, лежащую в области 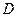, то эти две функции тождественно равны, изображение 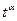и правой часть равенства (21.6) аналитичны в полуплоскости Rе 
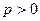, следовательно, совпадая в положительных точках, они совпадают на всей полуплоскости Rе 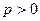(заметим, что степенные функции 
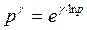комплексного переменного 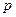многозначны при нецелых 
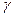, но, рассматривая их на полуплоскости Rе 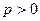, мы всякий раз имеем в виду те их ветви, которые происходят от ветвей 
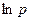, совпадающих для положительных 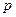с 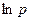). Итак,
≒
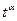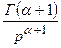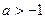() (21.7)
Так, при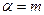 
≒
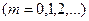
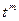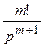(21.8)
и, в частности, при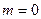 
1≒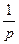
(21.9)
Из (21.8) по правилу смещения изображений (1.2 свойство 9 -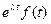 
≒
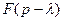) находим при любом целом неотрицательном 
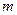и любом комплексном 
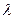l
≒
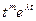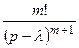(21.10)
и, в частности, при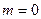
≒
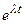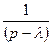(21.11)
2. Изображения тригонометрических и гиперболических функций. В силу (21.10) имеем:
≒
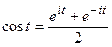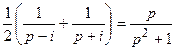(21.12)
≒
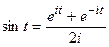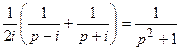(21.13)
≒
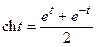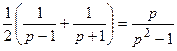(21.14)
≒
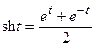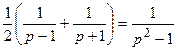(21.15)
Из (21.12) и (21.13) по правилу подобия (1.2, свойство 3 -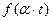 
≒ 
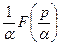) находим:
≒
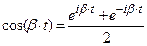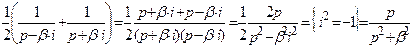(21.16)
≒
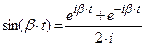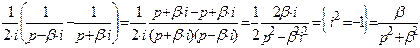(21.17)
откуда по правилу смещения изображений (1. 2, свойство 9 -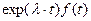 
≒ )
≒
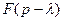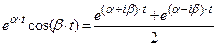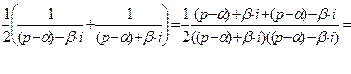
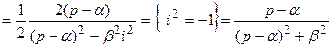(21.18)
≒
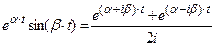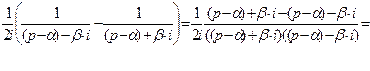
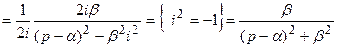(21.19)
