Теорема. При свертывании оригиналов изображения перемножаются, т.е. если  ≒
≒ и
и 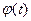 ≒
≒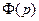 , то
, то 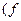 *
*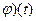 ≒
≒ 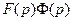 .
.
Доказательство. Для простоты мы имеем в виду лишь непрерывные на 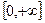 оригиналы. Учитывая формулу (19.4), достаточно показать, что
оригиналы. Учитывая формулу (19.4), достаточно показать, что
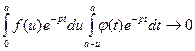 при
при 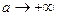 .
.
Пусть 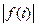 ≒
≒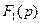 и
и 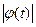 ≒
≒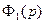 ,тогда, если Rе
,тогда, если Rе 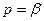 больше показателей роста
больше показателей роста  и
и 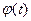 , то
, то
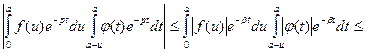
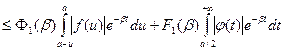 ,
,
что 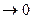 при
при 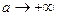 , что и требовалось доказать.
, что и требовалось доказать.
Пример. Найти свертку 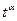 и
и 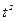 , где
, где 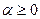 ,
, 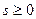 . Делая в интеграле подстановку
. Делая в интеграле подстановку 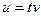 и учитывая формулы
и учитывая формулы
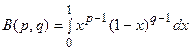 и
и 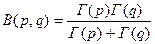
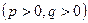 ,
,
где 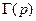 и
и 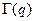 – гамма-функции, или эйлеровы интегралы 2-го рода, которые определяются для положительных значений независимых переменных
– гамма-функции, или эйлеровы интегралы 2-го рода, которые определяются для положительных значений независимых переменных 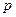 и
и 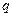 формулами:
формулами:
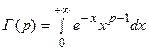 и
и 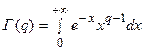
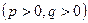 ,
,
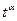 *
*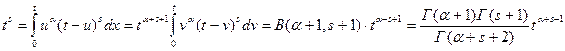
и, в частности, при целых неотрицательных 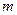 ,
, 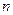
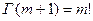 и
и 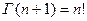
Следовательно, искомая свертка имеет вид
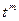 *
*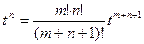 .
.
Формула Дюамеля. Пусть  - непрерывный на
- непрерывный на 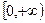 оригинал,
оригинал, 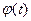 - непрерывно дифференцируемая на
- непрерывно дифференцируемая на 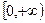 функция такая, что
функция такая, что 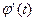 есть оригинал. Из
есть оригинал. Из  ≒
≒ и
и 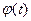 ≒
≒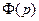 следует:
следует:
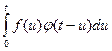 ≒
≒ 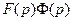
Из правила дифференцирования интегралов, зависящих от параметра, следует, что левая часть непрерывно дифференцируема на 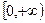 , причем
, причем
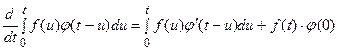
Отсюда в силу свойства 4 (см. 21.2) [дифференцирование оригинала 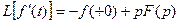 ] получаем искомую формулу Дюамеля
] получаем искомую формулу Дюамеля
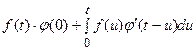 ≒
≒ 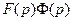 (21.5)
(21.5)
 2014-02-12
2014-02-12 1728
1728








