Приложения к решению линейных дифференциальных уравнений с постоянными коэффициентами
Лекция 22. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В случае, когда требуется найти решение неоднородного уравнения
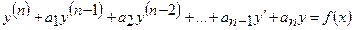 , (22.1)
, (22.1)
удовлетворяющего начальным условиям:
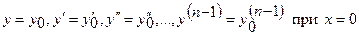 , (22.2)
, (22.2)
где 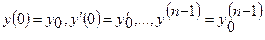 любые заданные числа, то для нахождения частного решения уравнения (22.1) можно воспользоваться преобразованием Лапласа.
любые заданные числа, то для нахождения частного решения уравнения (22.1) можно воспользоваться преобразованием Лапласа.
Найдем сначала изображение 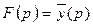 решения
решения 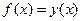 . С этой целью возьмем изображения обеих частей уравнения (22.1), применив к ним преобразование Лапласа и, используя правило дифференцирования оригинала (свойство 4). При этом получим уравнение линейное относительно
. С этой целью возьмем изображения обеих частей уравнения (22.1), применив к ним преобразование Лапласа и, используя правило дифференцирования оригинала (свойство 4). При этом получим уравнение линейное относительно 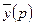 :
:
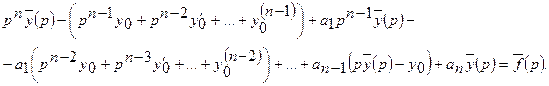
Разрешим это уравнение относительно 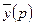 . Собрав все члены, содержащие
. Собрав все члены, содержащие 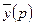 , и перенеся остальные члены в правую часть, получим
, и перенеся остальные члены в правую часть, получим
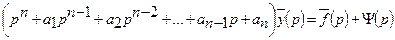 , (22.3)
, (22.3)
где
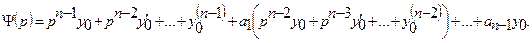
Необходимо отметить, что коэффициент при 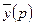 есть не что иное, как характеристический полином
есть не что иное, как характеристический полином 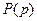 для однородного линейного уравнения, соответствующего уравнению (22.1). Поэтому уравнение (22.3) можно записать в виде:
для однородного линейного уравнения, соответствующего уравнению (22.1). Поэтому уравнение (22.3) можно записать в виде:
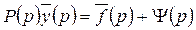 . (22.4)
. (22.4)
Это уравнение называется изображающим уравнением или операциьнным уравнением для задачи Коши (22.1), (22.2).
Из уравнения (22.4) находим изображение искомого решения
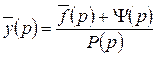 . (22.5)
. (22.5)
Восстанавливая по изображению (22.5) оригинал (например, по табл. 1), получим искомое решение 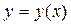 .
.
Пример 22.1. Найти решение уравнения: 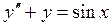 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 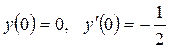
Возьмем изображение обеих частей исходного уравнения. Если оригиналу 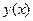 соответствует изображение
соответствует изображение 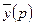 , что записывается следующим образом –
, что записывается следующим образом – 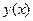
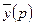 , то можно использовать правило дифференцирования оригинала. В нашем случае в левой части исходного уравнения мы имеем сам оригинал
, то можно использовать правило дифференцирования оригинала. В нашем случае в левой части исходного уравнения мы имеем сам оригинал 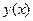 и его вторую производную
и его вторую производную 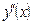 . Представим изображение
. Представим изображение 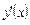
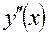 ≒
≒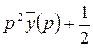 ,
,
тогда изображение левой части исходного уравнения будет иметь вид:
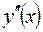 + у(х) ≒
+ у(х) ≒ 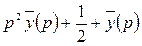 ,
,
а изображение правой части, которое можно взять из таблицы оригиналов и изображений (табл.1) будет выглядеть так
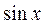 ≒
≒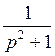 .
.
Поэтому изображающим или операторным уравнением будет уравнение
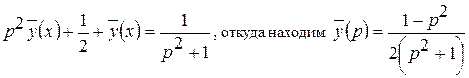 . (П22.1.1)
. (П22.1.1)
По таблице оригиналов и изображений (табл.1) устанавливаем, что функция (П22.1.1) является изображением функции 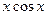 с точностью до множителя (-1/2). Поэтому искомым решением исходной задачи Коши будет
с точностью до множителя (-1/2). Поэтому искомым решением исходной задачи Коши будет
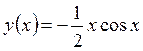 .
.
Пусть функция f(t) удовлетворяет следующим условиям:
1) f(t) кусочно непрерывна на отрезке [0, а ] для любого a > 0;
2) f(t) = 0 при t < 0;
3) существуют числа М > 0 и s 0 ≥ 0 такие, что 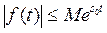 .
.
Тогда преобразованием Лапласа функции f(t) называется функция
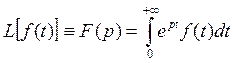
где р = s + iσ; обозначение: f(t)= F(p).
Очевидно, преобразование Лапласа существует, если s > s 0 (при этом несобственный интеграл сходится).
Основными свойствами преобразования Лапласа являются:
1) линейность, т. е. 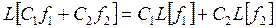 , где С 1и С 2— постоянные;
, где С 1и С 2— постоянные;
2) преобразование частных производных по такому правилу: если u = u (x,t) и преобразование Лапласа проводится по переменной t (t ≥ 0), то, обозначив
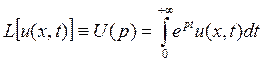
можно (интегрированием по частям) установить соотношения при определенных условиях на функцию u (x,t) и ее частные производные
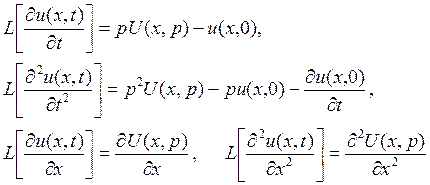
Таким образом, преобразование Лапласа заменяет операцию дифференцирования по временной переменной t умножением. Этот важный факт используется при решении дифференциальных уравнений с частными производными.
Рассмотрим теперь, как применяется преобразование Лапласа к решению гиперболических задач.
Пример 22.2. Начиная с момента t = 0 к концу х = 0 полубесконечной изолированной электрической линии подключена э.д.с. E(t). Найти напряжение u(x,t) для t > 0 в линии, если начальное напряжение и начальный ток в ней равны нулю, для случаев, когда:
а) линия без потерь (R = G = 0);
б) линия без искажения (RC = LG).
Решение случая а).
Математическая постановка задачи для случая а) имеет вид
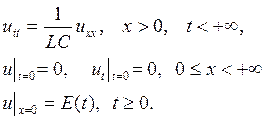
здесь L и С — соответственно индуктивность и емкость единицы длины провода.
Применим преобразование Лапласа по временной переменной t к левой и правой частям дифференциального уравнения с частными производными. Тогда, учитывая, что
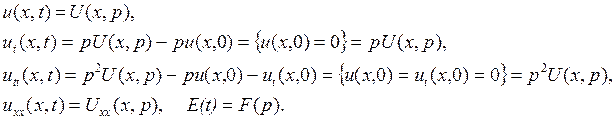 Из исходного уравнения получим обыкновенное дифференциальное уравнение
Из исходного уравнения получим обыкновенное дифференциальное уравнение
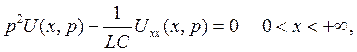
с граничными условиями
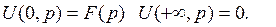
(второе граничное условие следует из физических соображений).
Итак, имеем граничную задачу
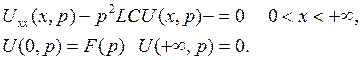
Общее решение нашего уравнения есть
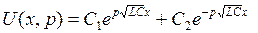 ,
,
где С 1и С 2— произвольные постоянные. Сразу отметим, что нужно полагать С 1= 0 (иначе U(x,p) →∞ при х →∞). Поэтому
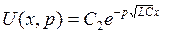 .
.
Полагая здесь х = 0, находим U( 0 ,p) = С 2. Однако в соответствии с граничным условием условию U( 0 ,p) = F(p). Значит, С 2 = F(p). Следовательно,
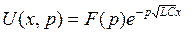
С учетом свойства запаздывания: если f(t) ← F(p), то f(t-τ)←exp(-рτ)F(p). Отсюда, возвращаясь к оригиналу, получим
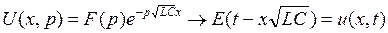 .
.
Необходимо отметить, что
при  ,
,
а при 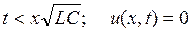
Решение случая б).
Математическая постановка задачи имеет вид
б) 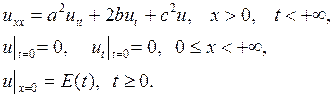
где a 2 = LC, b = ½(CR + LG), c 2 = RG (здесь R и G — сопротивление и проводимость единицы длины провода).
Применяя преобразование Лапласа, получим граничную задачу
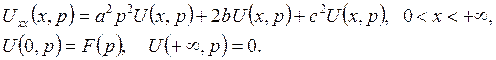
Общее решение уравнения имеет вид
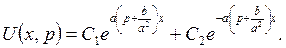
Из граничного условия U (+∞,p) = 0 следует, что С 1= 0. Значит,
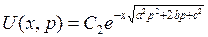
Если 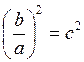 , то тогда
, то тогда
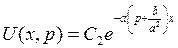
Из граничного условия 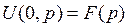 , следует
, следует
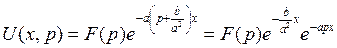
С учетом свойства запаздывания: если f(t) ← F(p), то f(t-τ)←exp(-рτ)F(p). Отсюда, возвращаясь к оригиналу, получим
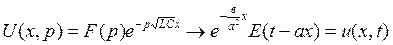 .
.
Необходимо отметить, что
при 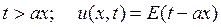 ,
,
а при 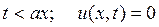
Пример 22.3. Решить краевую задачу
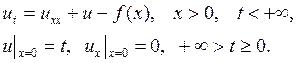 (П22.3.1)
(П22.3.1)
Решение. Воспользуемся преобразованием Лапласа по переменной х. Учитывая свойство этого преобразования, имеем
u(x,t) ≒ p 2 U(p,x),
ut(x,t) ≒ Ut(p,x),
ux(x,t) ≒ pUt(p,t) - t,
uxx(x,t) ≒ p2U(p,t) - pt, f(x) ≒ F(p).
Из уравнения (П22.3.1), применяя к левой и правой его частям преобразование Лапласа, находим
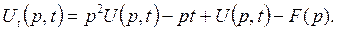
Мы получили обыкновенное дифференциальное уравнение первого порядка (в этом уравнении р играет роль параметра) по переменной t. Его можно переписать так:
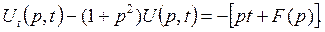
Общее решение этого уравнения есть функция
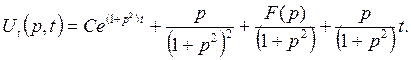
Заметим теперь, что постоянную С здесь нужно считать равной нулю, ибо если С ≠0, то U(p, t) → ∞ при р → ∞ (нарушается необходимое условие существования изображения). Таким образом,
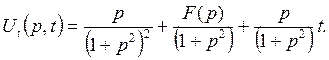
Теперь осталось вернутся к оригиналу u (х, t). Имеем
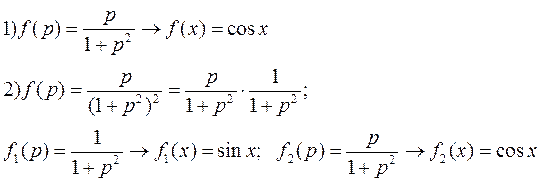
и по теореме о свертке получим
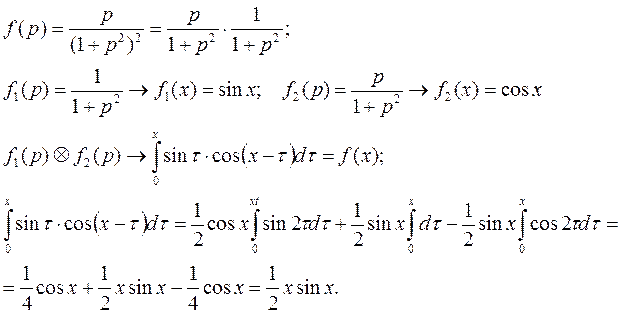
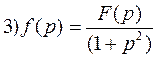
и по теореме о свертке получим
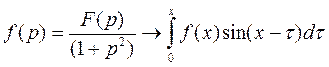
Следовательно, решение нашей задачи есть
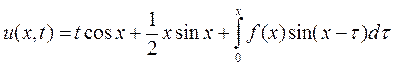 .
.
 2014-02-12
2014-02-12 4657
4657
