1. Для изображения регулярного в бесконечности.
Для того чтобы изображение было регулярно в бесконечно удаленной точке, необходимо и достаточно, чтобы оригинал являлся целой функцией экспоненциального типа.
Определим понятие целой функцией экспоненциального типа. Итак, целая функция 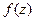 комплекснозначного переменного
комплекснозначного переменного 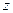 называется целой функцией экспоненциального типа, если можно найти такие положительные числа
называется целой функцией экспоненциального типа, если можно найти такие положительные числа 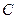 и
и 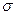 , чтобы для всех комплексных значений
, чтобы для всех комплексных значений 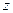 выполняется неравенство
выполняется неравенство
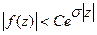 . (21.24)
. (21.24)
Существует также лемма, которая доказывает, что для того чтобы степенной ряд
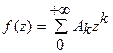 , (21.25)
, (21.25)
изображал целую функцию экспоненциального типа, необходимо и достаточно, чтобы для некоторых чисел 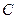 и
и 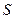 выполнялись неравенства
выполнялись неравенства
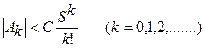 . (21.26)
. (21.26)
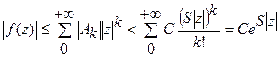 ,
,
Необходимо отметить, что операции линейного комбинирования, умножения на независимое переменное, умножения на показательную функцию, линейного преобразования независимого переменного, дифференцирования и интегрирования, примененные к целым функциям экспоненциального типа, приводят снова к целым функциям экспоненциального типа.
Приведенная лемма позволяет реализовать доказательную базу приведенного выше утверждения о том, что для того чтобы изображение было регулярно в бесконечно удаленной точке, необходимо и достаточно, чтобы оригинал являлся целой функцией экспоненциального типа.
Необходимо отметить, что всякая регулярная в бесконечности аналитическая функция, равная нулю в бесконечности, является изображением некоторой целой функции экспоненциального типа. Из этого замечания заключаем, что с помощью преобразования Лапласа устанавливается взаимно однозначное соответствие между всеми целыми функциями экспоненциального типа и всеми аналитическими функциями, регулярными в бесконечно удаленной точке и равными в ней нулю.
2. Нахождение оригинала по его изображению (когда оно регулярно в бесконечности).
Предыдущим изложением показано, что если  – какая-нибудь аналитическая функция, регулярная в бесконечно удаленной точке и равная в ней нулю, и если ее разложение в виде
– какая-нибудь аналитическая функция, регулярная в бесконечно удаленной точке и равная в ней нулю, и если ее разложение в виде 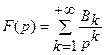 ряда Лорана в окрестности бесконечности, то выражение
ряда Лорана в окрестности бесконечности, то выражение
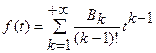 (21.27)
(21.27)
будет оригиналом, имеющим изображение вида -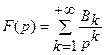 .
.
3. Изображение бесселевых функций.
Функция Бесселя 1-го рода 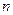 -го порядка, являющаяся первым частным решением уравнения Бесселя при
-го порядка, являющаяся первым частным решением уравнения Бесселя при 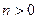 имеет вид:
имеет вид:
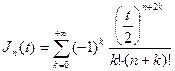
или
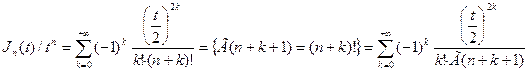 .
.
Следовательно, можно утверждать, что функция 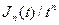 является целой функцией экспоненциального типа вида -
является целой функцией экспоненциального типа вида - 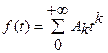 , у которой
, у которой 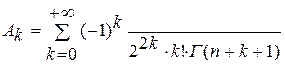 . Таким образом, изображение этой функции определяется формулой (1.29) -
. Таким образом, изображение этой функции определяется формулой (1.29) - 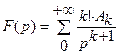 . Поэтому изображение будет иметь вид:
. Поэтому изображение будет иметь вид: 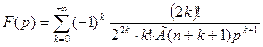 , и окончательно получим
, и окончательно получим
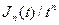 ≒
≒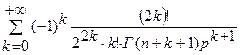 .
.
При 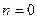 получим
получим
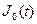 ≒
≒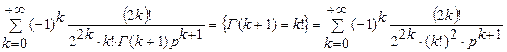
С другой стороны, биномиальное разложение правой части приводит изображение к виду
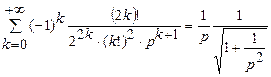 ,
,
следовательно, получим
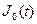 ≒
≒ .
.
Используя метод индукции можно записать изображение бесселевой функции при любом положительном n:
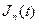 ≒
≒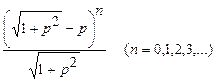 (21.28)
(21.28)
Если изображение  имеет вид
имеет вид 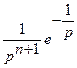 , то этому изображению соответствует оригинал вида:
, то этому изображению соответствует оригинал вида:
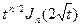 ≒
≒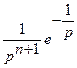 (21.29)
(21.29)
и при 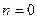
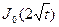 ≒
≒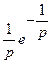 .
.
В таблице 21.1 приведены наиболее часто встречающиеся оригиналы функций и соответствующие им изображения.
Таблица 21.1.
Оригинал –  | Изображение –  | |
| 1. | 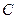 ( (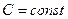 ) ) | 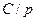 |
| 2. | 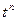 ( (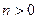 , целое) , целое) | 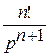 |
| 3. | 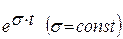 | 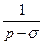 |
| 4. | 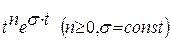 | 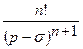 |
| 5. | 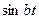 ( (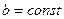 ) ) |  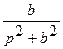 |
| 6. | 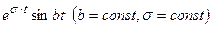 | 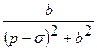 |
| 7. | 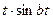 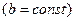 | 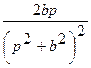 |
| 8. | tn sin bt 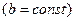 | 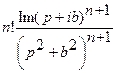 |
| 9. | 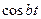 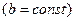 | 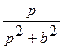 |
| 10. | 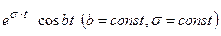 | 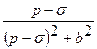 |
| 11. | 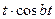 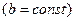 | 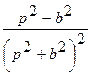 |
| 12. | 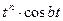 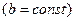 | 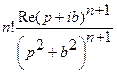 |
| 13. | 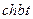 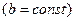 | 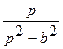 |
| 14. | 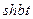 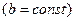 | 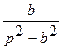 |
| 15. | 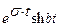 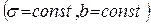 | 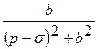 |
| 16. | 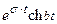 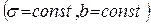 | 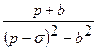 |
| Продолжение табл. 21.1 | ||
| 17. | 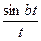 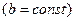 | 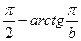 |
| 18. | 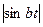 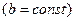 | 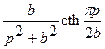 |
| 19. | 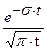 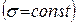 | 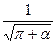 |
| 20. | 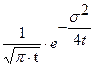 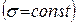 | 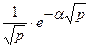 |
| 21. | 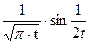 | 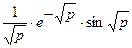 |
| 22. | 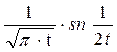 | 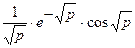 |
| 23. | 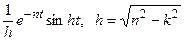 | 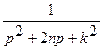 |
| 24. | 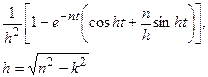 | 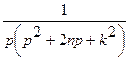 |
| 25. | 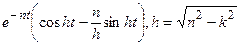 | 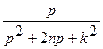 |
| 26. | 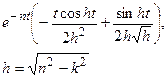 | 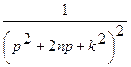 |
| 27. | 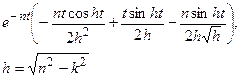 | 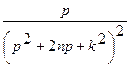 |
 2014-02-12
2014-02-12 1092
1092








