В основу миграционной подмодели положены три взаимосвязанные модельных блока:
- блок диффузионной модели,
- блок модели адвекции-диффузии (модель одиночной трещины);
- блок модели биосферы.
Диффузионная модель описывает перенос радионуклидов в однородном вмещающем массиве с учетом источникового члена и радиоактивного распада посредством диффузионного механизма. Механизм высвобождения радиоактивности из отвержденной формы отходов может быть описан несколькими моделями. Остановимся на четырех, которые далее обсуждаются в порядке усложнения.
Модель №1. Модель мгновенного растворения предполагает мгновенное высвобождение активности в поровую воду отвержденных отходов - 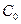 . Типичными представителями элементов, характеризующихся высокой растворимостью являются цезий и йод. В контексте нашей проблемы это могут быть, например, изотопы -
. Типичными представителями элементов, характеризующихся высокой растворимостью являются цезий и йод. В контексте нашей проблемы это могут быть, например, изотопы - 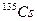 и
и 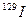 . Строго говоря, данная модель может быть применена не только к элементам с высокой растворимостью. Но для этого необходимо с учетом принимаемой модели адсорбции проконтролировать полную активность изотопа и предоставляемый отходам объем порового пространства с численным значением предела растворимости элемента.
. Строго говоря, данная модель может быть применена не только к элементам с высокой растворимостью. Но для этого необходимо с учетом принимаемой модели адсорбции проконтролировать полную активность изотопа и предоставляемый отходам объем порового пространства с численным значением предела растворимости элемента.
Модель №2. Модель предела растворимости предполагает, что концентрация радионуклидов на границе раздела кондиционированной формы отходов и скальной породы лимитируется величиной элементной растворимости его определенной химической формы - 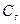 . Такая модель считается справедливой для достаточно большого числа долгоживущих радионуклидов, например, изотопы плутония
. Такая модель считается справедливой для достаточно большого числа долгоживущих радионуклидов, например, изотопы плутония 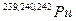 и урана
и урана 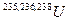 .
.
Модель №3. Простейшая модель выщелачивания, которая предполагает знание помимо предела элементной растворимости 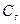 еще и скорости выщелачивания активности
еще и скорости выщелачивания активности 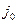 из матрицы отвержденной формы отходов, задаваемой в этой моделе постоянной.
из матрицы отвержденной формы отходов, задаваемой в этой моделе постоянной.
Модель №4. Двухкомпонентная модель выщелачивания, которая предполагает наличие разных скоростей выщелачивания активности из матрицы отходов 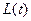 : «быструю» компоненту с периодом высвобождения порядка 1100 лет и «медленную» компоненту с периодом высвобождения около 22000 лет.
: «быструю» компоненту с периодом высвобождения порядка 1100 лет и «медленную» компоненту с периодом высвобождения около 22000 лет.
Следует отметить тот факт, что четвертая модель справедлива только для остеклованных РАО, а первые три модели, в принципе, могут быть использованы и для других форм отверждения отходов (цементная, битумная, керамическая матрицы).
Модель адвекции-диффузии применяется для расчета переноса радионуклидов по трещинам постоянной гидравлической апертуры 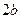 с потоком подземной воды. При этом скорость ламинарного потока в трещинах
с потоком подземной воды. При этом скорость ламинарного потока в трещинах 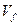 определяется посредством известного соотношения, справедливого для ламинарного течения между параллельными пластинами через коэффициент гидравлической проводимости трещины
определяется посредством известного соотношения, справедливого для ламинарного течения между параллельными пластинами через коэффициент гидравлической проводимости трещины 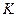 и градиент напора
и градиент напора
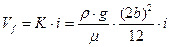
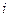 (23.1)
(23.1)
где 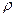 - плотность жидкости;
- плотность жидкости;
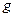 - ускорение свободного падения;
- ускорение свободного падения;
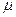 - динамическая вязкость.
- динамическая вязкость.
Биосферная модель описывает разбавление радионуклидов в биосфере и результирующие радиологические последствия при потреблении человеком загрязненной питьевой воды. Таким образом, рассматривается только внутреннее облучение населения через питьевую воду, как наиболее важную траекторию попадания радионуклидов в организм человека. Учитывая направленность пособия, эта модель подробно не описывается.
Диффузионная модель
В основе модели лежит обоснованное предположение, что отходы будут захоронены в стабильные геологические формации (типа гранита), не имеющие в области хранилища крупных протяженных трещин. Такое допущение позволяет рассматривать вмещающий массив в ограниченном масштабе площадки, как гомогенный, и моделировать перенос радионуклидов в этой области при доминирующем диффузионном механизме.
Единицей захоронения считается один контейнер, содержащий кондиционированные РАО или ОЯТ. Время разрушения контейнера (время начала высвобождения радионуклидов) 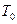 , после которого контейнер уже не обеспечивает своей защитной функции, оценивается через скорость коррозии металла при его взаимодействии с подземными водами. Известен целый ряд исследований, посвященных определению скорости коррозии металлических контейнеров (стальных, медных) с РАО. Все они свидетельствуют, что выбор величины скорости коррозии на уровне 0,01 мм/год представляется разумным. При вступлении кондиционированных отходов в контакт с подземными водами начинается высвобождение радионуклидов в результате процесса выщелачивания.
, после которого контейнер уже не обеспечивает своей защитной функции, оценивается через скорость коррозии металла при его взаимодействии с подземными водами. Известен целый ряд исследований, посвященных определению скорости коррозии металлических контейнеров (стальных, медных) с РАО. Все они свидетельствуют, что выбор величины скорости коррозии на уровне 0,01 мм/год представляется разумным. При вступлении кондиционированных отходов в контакт с подземными водами начинается высвобождение радионуклидов в результате процесса выщелачивания.
В сферической системе координат управляющее дифференциальное уравнение, описывающее диффузионный перенос растворенной в воде порового пространства радиоактивности с учетом радиоактивного распада, а также типичные начальное и граничное (на бесконечности) условия, имеют вид:
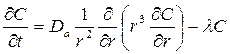 , ,
| (23.2) |
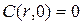 для для  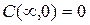 , ,
| (23.3) |
где 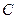 - концентрация радиоактивного вещества, растворенного в воде порового пространства;
- концентрация радиоактивного вещества, растворенного в воде порового пространства;
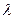 - постоянная распада;
- постоянная распада;
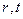 - пространственная и временная координаты;
- пространственная и временная координаты;
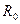 - радиус контейнера (источника);
- радиус контейнера (источника);
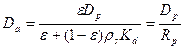 - наблюдаемый коэффициент диффузии;
- наблюдаемый коэффициент диффузии;
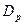 - коэффициент диффузии радионуклида по обводненному поровому пространству породы, который определяется посредством выражения
- коэффициент диффузии радионуклида по обводненному поровому пространству породы, который определяется посредством выражения 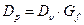 ;
;
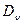 - молекулярный коэффициент диффузии ионов в свободной воде;
- молекулярный коэффициент диффузии ионов в свободной воде;
 - геометрический фактор, определяемый через
- геометрический фактор, определяемый через 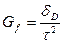 , где
, где 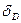 и
и 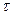 - сжимаемость и извилистость пор, соответственно;
- сжимаемость и извилистость пор, соответственно;
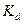 - коэффициент распределения, т.е. используем приближение линейной изотермы адсорбции;
- коэффициент распределения, т.е. используем приближение линейной изотермы адсорбции;
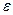 и
и 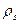 - пористость и плотность «скелета» породы, причем
- пористость и плотность «скелета» породы, причем 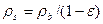 , где
, где 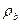 - насыпная плотность породы в сухом состоянии;
- насыпная плотность породы в сухом состоянии;
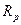 - коэффициент задержки в матрице породы.
- коэффициент задержки в матрице породы.
Отдельным образом опишем граничное условие на левой границе для перечисленных выше моделей высвобождения активности.
 2014-02-12
2014-02-12 401
401








