Модель №3

Модель №2

Модель №1

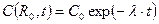(23.4)

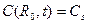(23.5)

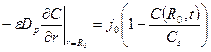(23.6)

Модель №4

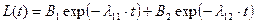(23.7)

где , ; , , ;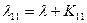

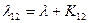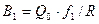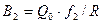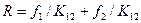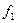и 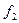- доли «быстрой» и «медленной» компонент выщелачивания;

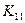и 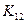- коэффициенты скорости выщелачивания соответствующих компонент;

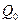- начальная активность радионуклида в отвержденной форме.

Таким образом, предстоит в рамках диффузионного переноса пошагово решить следующие четыре задачи, каждая из которых описывается несколькими уравнениями:

- первая - (23.2)-(23.3) и (23.4);

- вторая - (23.2)-(23.3) и (23.5);

- тертья - (23.2)-(23.3) и (23.6) и

- четвертая - (23.2)-(23.3) и (23.7).

Оказывается, что несколько шагов при решении указанных задач совпадают. Проделаем последовательно общие шаги.

Первый шаг. Вводим новую функцию 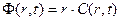. Тогда уравнение (23.2) может быть переписано в виде (авторы рекомендуют читателю проверить «руками» такое преобразование)

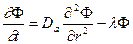(23.8)

Второй шаг. К уравнению (23.8) применяем преобразование Лапласа 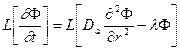(23.9)

С учетом основной теоремы операционного метода и начального нулевого распределения концентрации, выражение (23.9) в переменных изображения принимает вид

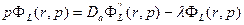
или

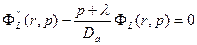(23.10)

Третий шаг. Ищем решение уравнения (23.10). В общем виде решение этого уравнения имеет стандартный вид

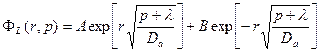
Из граничного условия на правой границе (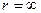) естественно записать 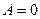. Таким образом, вид решения уравнения (23.10) довольно простой

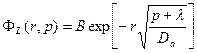(23.11)

Осталось определить константу 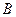, для чего и будем использовать левое граничное условие – при .

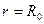Естественно, что теперь необходимо работать с конкретным граничным условием. При этом необходимо помнить, что

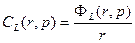(23.12)

Четвертый шаг для граничного условия (23.4). Применим к нему преобразование Лапласа.

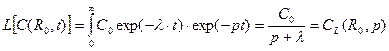
С другой стороны, учитывая (23.11) и (23.12), имеем

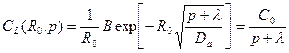
Откуда легко получается выражение для коэффициента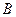

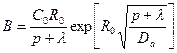
Теперь уже есть возможность окончательно записать функцию (23.12)

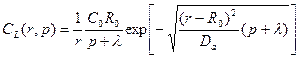(23.13)

Теперь, обратившись к таблицам обратного преобразования Лапласа, есть возможность записать искомую функцию в переменных оригинала

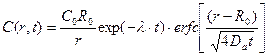(23.14)

Четвертый шаг для граничного условия (23.5). Применим к нему преобразование Лапласа.

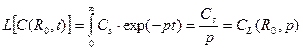
С другой стороны, учитывая (22.11) и (22.12), имеем

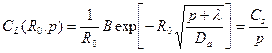
Откуда легко получается выражения для коэффициента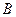

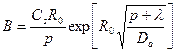
Теперь уже есть возможность окончательно записать вид функции (23.12)

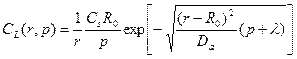(23.15)

Обращаемся к таблицам обратного преобразования Лапласа и записываем искомую функцию в переменных оригинала

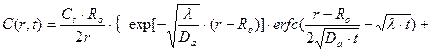
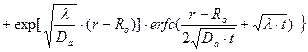(23.16)

Четвертый шаг для граничного условия (23.6). Вычислим первую производную функции (23.12) 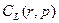по пространственной координате

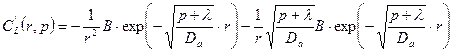
Теперь применим преобразование Лапласа к граничному условию (23.6), используя при этом соответствующие свойства преобразования

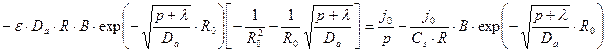
Откуда легко плучается выражения для коэффициента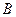

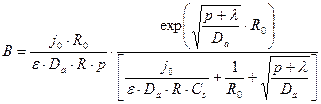
Теперь уже есть возможность окончательно записать вид функции (23.12)

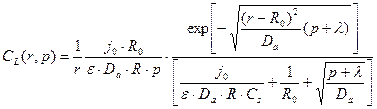(23.17)

Здесь удобно ввести обозначения.

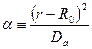
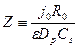
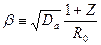
Теперь можно обратиться к таблицам обратного преобразования Лапласа (табл. 21.1) и записать искомую функцию в переменных оригинала

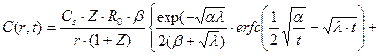
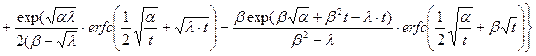(23.18)

Четвертый шаг для граничного условия (23.7). Константу 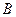определим из граничного условия на поверхности источника

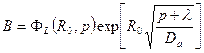
Тогда уравнение (23.11) примет вид

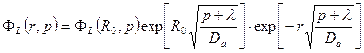(23.19)

Здесь необходимо записать уравнение баланса радиоактивности 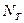во вмещающем массиве, что возможно с учетом используемого граничного условия (23.7)

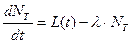(23.20)

Подставляем в уравнение (23.20) выражение для потока двухкомпонентной модели выщелачивания и снова воспользуемся преобразованием Лапласа 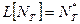. С учетом нулевого начального распределения радиоактивности получим

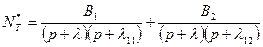(23.21)

С учетом (23.12) возвращаемся к балансу радиоактивности во вмещающем массиве, но уже в переменных изображения и в интегральной форме

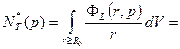
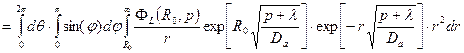(23.22)

Интеграл (23.22) не является самым сложным

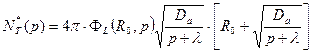
С учетом (23.21) получаем выражение для

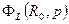
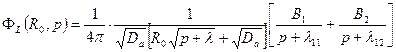(22.23)

Здесь удобно ввести обозначения с тем, чтобы выражение (23.23) записать в необходимой для дальнейших шагов форме, в частности

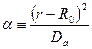
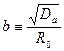
После указанной подстановки выражение (23.23) принимает вид

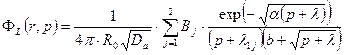(23.24)

Теперь можно обратиться к таблицам обратного преобразования Лапласа (табл 21.1) и записать искомую функцию в терминах оригинала для двухкомпонентной модели выщелачивания

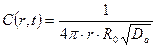
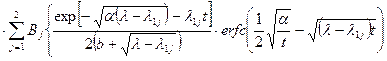
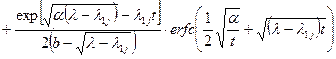
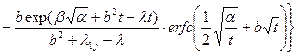(23.25)

К огромному сожалению, выражение (23.25) не может быть непосредственно использовано для вычислений, поскольку выражение 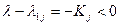. Предварительно, требуется кропотливо «поработать» над выражением (23.25) и выделить из него имеено вещественную часть. Но здесь будут использованы другие методы, а не преобразование Лапласа.

Обобщим результаты решения диффузионной задачи. Таким образом, можно констатировать следующее:

- выражение (23.14) является решением диффузионной задачи (23.2)-(23.3) с граничным условием (23.4) – модель мгновенного растворения;

- выражение (23.18) - с граничным условием (23.5) – модель предела растворимости;

- выражение (23.21) – с граничным условием (23.6) – простейшая модель выщелачивания;

- выражение (23.25) – с граничным условием (23.7) – двухкомпонентная модель выщелачивания.

Модель адвекции-диффузии

Для моделирования переноса радиоактивности по трещине была выбрана известная модель D.Tang и его коллег [6], так называемая модель одиночной трещины (рис.23.2). Приведенная ниже система уравнений (23.26)- (23.29) записана при следующих предположениях по геометрии и гидравлическим свойствам физической системы (рис. 23.3):

- ширина трещины много меньше ее длины;

- поперечная диффузия и дисперсия в пределах трещины гарантирует полное смешение потока поперек трещины. В пособии рассматривается и в миграционной подмодели программно реализован [1] вариант с нулевой дисперсией, что, как показали D. Tang и его коллеги, справедливо при скоростях движения воды по трещинам на уровне единиц метров в год;

- в матрице «работают» только диффузионные механизмы;

- перенос в трещине более быстрый, чем в матрице;

- некоторая часть радионуклидов диффундирует в микропоры матрицы породы вследствие различий концентрации на границе раздела трещина-матрица;

- гидрологические параметры постоянные;

- линейная изотерма адсорбции радионуклидов справедлива, как в матрице породы, так и на поверхности трещины.

Трещина

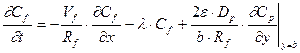(23.26) 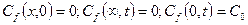(23.27)

матрица породы

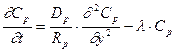(23.28) 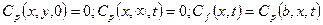(23.29)

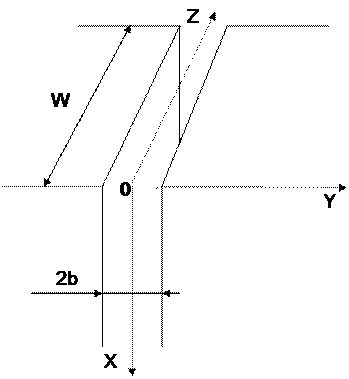
Рис. 23.2. Схематичное представление модели

где 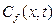- концентрация радиоактивного вещества, растворенного в воде трещины;

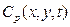- концентрация радиоактивного вещества, растворенного в воде порового пространства матрицы;

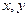- пространственные координаты;

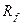- коэффициент задержки в трещине, который определяется следующим образом ;

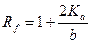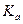- коэффициент поверхностной сорбции в трещине, имеющий размерность длины и определяемый как «масса растворенного вещества, адсорбируемая на единице площади поверхности и деленная на концентрацию растворенного вещества» ;

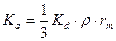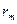- радиус мигрирующей частицы;

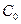- постоянное значение концентрации, задаваемое на входе в трещину. Относительно этой физической величины имеются определенные соображения, но, учитывая направленность пособия, здесь они не описываются.

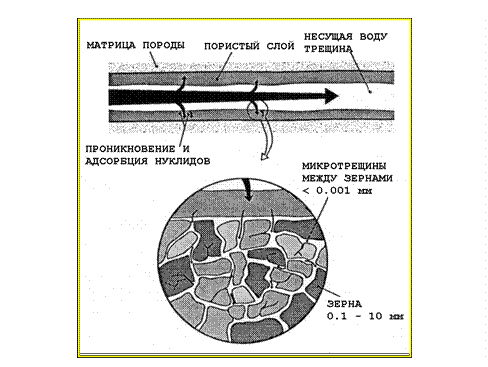
Рис.23.3. Модель одиночной трещины

Решение системы уравнений (23.26)-(23.29) получается методом преобразования Лапласа. К уравнениям (23.26) и (23.29) применям преобразование Лапласа и основную теорему этого метода. Тогда с учетом начального распределения активности в трещине и матрице получим

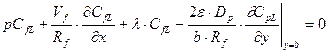
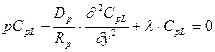
Для дальнейших шагов последние два уравнения удобно записать в другой форме

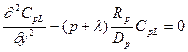(23.30) 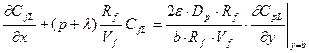(23.31)

Решение уравнения (23.30) ищем, как и ранее, в традиционном виде

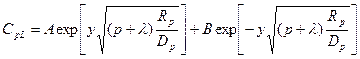
Из граничного условия на бесконечости (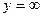) имеем 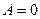, а поскольку стенка трещины имеет координату 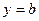, то решение ищется в виде

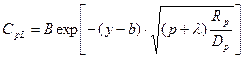(23.32)

Для упрощения дальнейших преобразований введем следующее обозначение 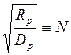. В этих обозначениях выражение (23.32) немного упрощается. Кроме того, напомним, что на стенке трещины справедливо условие 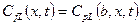. Но тогда выражение (23.32) принимает вид

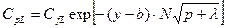(23.33)

Найдем производную функции 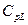на стенке

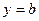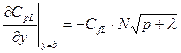() (23.34)

Теперь уравнение (23.31) можно переписать в виде

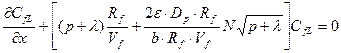
Через два новых обозначения 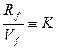и 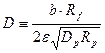последнее выражение существенно упрощается для выполнения последующих действий

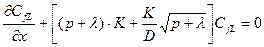(23.35)

Решение дифференциального уравнения первого порядка (23.35) с учетом граничного условия (23.27) – постоянства концентрации на входе в трещину – запишется в виде

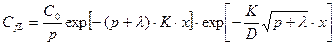(23.36)

Решение для концентрации в матрице породы в переменных изображения легко получается из комбинации уравнений (23.33) и (23.36). Если снова для упрощения формул ввести обозначение 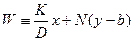, то решение для 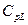примет вид

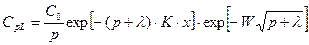(23.37)

Для выполнения обратного преобразования Лапласа с помощью табличных функций (например, [5]) оказывается удобно перейти для переменных изображения к следующему обозначению 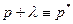. Тогда уравнения (23.36) и (23.37), соответственно, примут вид

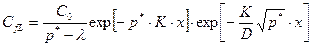(23.38)

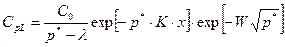(23.39)

Здесь на помощь приходит, первую очередь, основное функциональное соотношение обратного преобразования Лапласа

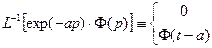при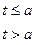

а во вторую очередь, позиция 23.124 [5]. Для заключительного шага удобны обозначения

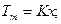
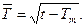
Решение исходной системы уравнений для функции 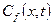, описывающей распределение концентрации радиоактивности в трещине и справедливое для условия 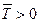, имеет вид:

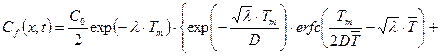
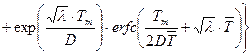(23.40)

а решение исходной системы уравнений для функции 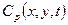, описывающей распределение концентрации радиоактивности в матрице породы и справедливое также для условия 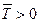, имеет вид:

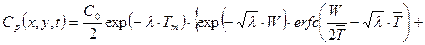
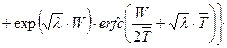(23.41)

Таким образом, уравнения (23.40) и (23.41) с указанными выше обозначениями являются рещением исходной системы уравнений в приближении модели одиночной трещины с постояным значением концентрации на входе в трещину.