Основные теоремы комбинаторики

2.1. Перестановки.

Число перестановок Р из n различных элементов (от французского слова permutation, что и означает перестановка) равно произведению всех натуральных чисел от 1 до n: Первый элемент в перестановке из n элементов можно выбрать n способами, второй (после выбора первого) можно выбрать (n-1) способами, третий – (n-2) способами и т. д. Перемножая способы выбора 1-го элемента со способами выбора 2-го, со способами выбора 3-го элемента и т. д, (принцип произведения) получим 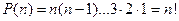способов. Таким образом, 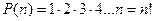При этом полагают 0! =1! = 1.

Пример. Назовём словом любую конечную последовательность букв русского алфавита без повторений. Сколько различных слов можно получить, переставляя буквы слова КНИГА? (Ясно, что все буквы различны. Буква К может занимать любое из 5 мест, но тогда буква Н может занимать любое из 4 мест и т.д. Таким образом, всего можно получить 5!=120 слов.)

Пример. В русском алфавите 33 различные буквы. Сколько слов, содержащих по 5 букв, можно составить, если не допускать слов, в которых две одинаковые буквы идут подряд? (Будем выбирать буквы одну за другой - сначала первую, потом вторую, третью, четвертую, пятую. Первую букву можно выбрать 33 способами - все 33 буквы русского алфавита. Вторую букву можно выбрать лишь 32 способами - ведь она должна отличаться от первой, третью букву можно выбрать тоже 32 способами - она должна отличаться от второй; четвертую и пятую буквы тоже можно выбрать 32 способами. А всего получается 33. 32 • 32 • 32 • 32 = 34 603 008 различных слов, удовлетворяющих поставленному условию.)

2.2.Перестановки с повторениями.

Пусть имеется множество, состоящее из n элементов, причем среди них n₁ элементов 1-го типа; n₂ элементов 2-го типа и т.д., n_k элементов k-гo типа, причем n_l+n₂+...+n_k =n. Число перестановок с повторениями из n элементов обозначают 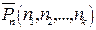и вычисляют по формуле .

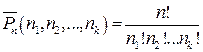Её можно получить так: если бы все n элементов были различными, число перестановок из них равнялось бы n! Чтобы исключить из них перестановки, полученные перестановками одинаковых элементов, разделим на произведение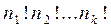

Пример. Сколько различных слов можно получить, переставляя буквы слова МАТЕМАТИКА? (Ясно, что если бы все буквы были бы различны, то таких слов было бы 10!. Но буква А повторяется 3 раза, а буквы М и Т по 2 раза. Таким образом, всего можно получить 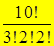слов.)