Z(x2-z2-a2)/((x2+z2-a2)2+4a2z2)

Если соотношения геометрических характеристик а, х, z в этих формулах представить в виде коэффициента влияния К_z, то можно записать: σ_z=K_zp .

Коэффициент влияния К_z зависят от безразмерных параметров х/b и z/b, где х и z — координаты точки, в которой определяются напряжения, b=2а — ширина полосы загружения. Значения этих коэффициентов приведены в табл. 5.1.

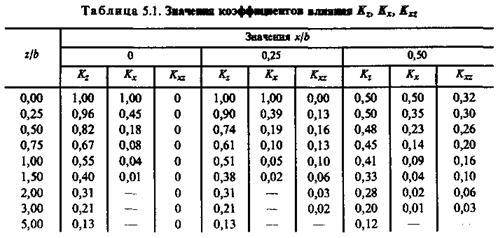
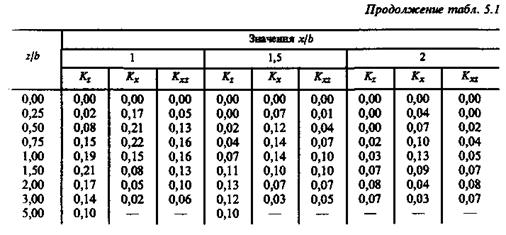
Зная ширину фундамента b и задавшись координатами точки, в которой требуется определить напряжения, можно вычислить безразмерные параметры для этой точки и по данным таблицы определить соответствующие коэффициенты влияния. Затем при известной величине интенсивности нагрузки р по формуле найти значение напряжения σ_z в заданной точке.

Рассчитанные таким образом величины σ_z представлены на рис. 5.8, а слева в виде линий равных напряжений (изолиний напряжений) и справа в виде эпюры этих напряжений по вертикальной оси, проходящей через центр площади фундамента.

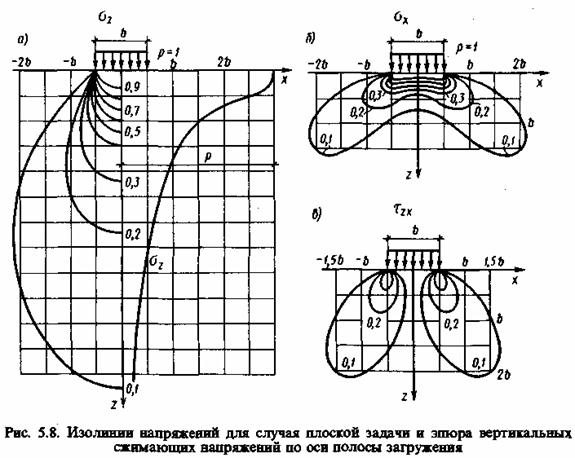
Аналогичные решения получены и для других видов нагрузок (например, треугольной, параболической и т д.). Соответствующие коэффициенты влияния приведены в табличной форме в различных источниках (в частности, в учебниках Н. А. Цытовича по механике грунтов). Используя эти таблицы, можно самую сложную форму нагрузки представить как комбинацию простейших эпюр, рассчитать в требуемой точке
напряжения от каждой эпюры и, используя принцип суперпозиции, определить в этой точке суммарное напряжение от полной нагрузки.

Пространственная задача. Действие равномерно распределенной нагрузки. Условия пространственного напряженного состояния в основании возникают тогда, когда по его поверхности действует местная нагрузка, распределенная по площади квадрата, прямоугольника, круга, эллипса и т. п. В этом случае неизвестными являются все компоненты напряжений. Для ряда таких задач имеются решения, полученные в замкнутом виде.

Значения вертикальных сжимающих напряжений σ_z в любой точке основания от действия нагрузки интенсивностью р, равномерно распределенной по площади прямоугольника размером lхb, впервые были получены А. Лявом в 1935 г. Практический интерес представляют компоненты напряжений σ_zC, относящиеся к вертикали, проведенной через угловую точку С этого прямоугольника, и σ_z_О, действующие по вертикали, проходящей через его центр (рис. 5.9).

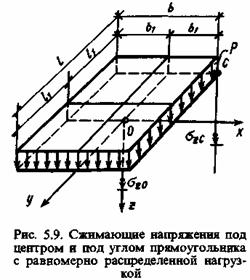
Используя введенные выше понятия коэффициентов влияния, можно записать:

σ_zC=K_zCp; σ_zO=K_zOp ,

где K_zC и K_zO – соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точки, в которой определяются напряжения.

Между значениями σ_zC и σ_zC имеется определенное соотношение. Можно показать, что напряжения в точках, расположенных на вертикали, проходящей через центр площади загружения, равны учетверенным значениям угловых напряжений, действующих на удвоенной глубине, т. е.

σ_zO=4σ_2z,_C

Тогда оказывается удобным выразить формулы σ_zC=K_zCp; σ_zO=K_zOp через общий коэффициент влияния α и записать их в виде

σ_zC=1/4αp; σ_zO=αp.

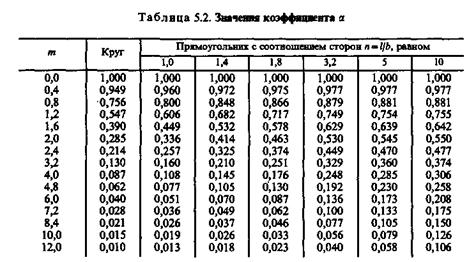
Коэффициент α зависит от безразмерных параметров m и n. Параметр n=l/b для обоих случаев является одинаковым. Следует помнить, что при определении углового
напряжения σ_zC параметр m=z/b, при определении напряжения под центром прямоугольника σ_zO параметр m=2z/b. Значения коэффициентов α приведены в табл. 5.2. Здесь же даны значения коэффициента α для определения сжимающих напряжений под центром нагрузки, равномерно распределенной по площади круга радиусом r=(π/A)^1/2, причем m=2z/r.

Приведенные выражения позволяют определить сжимающие напряжения в основании не только под центром или углом прямоугольной площадки загружения, но и по вертикали, проходящей через любую точку поверхности. Для этого применяется метод угловых точек. Здесь возможны три варианта решения (рис. 5.10).

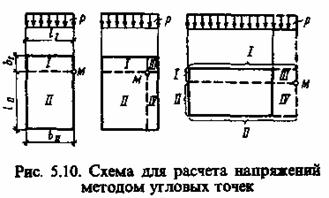
Пусть вертикаль проходит через точку М, лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения σ_zM как сумму угловых напряжений I и II прямоугольников, т. е. σ_zM=σ^I_zC+σ^II_zC .

Соответственно значения напряжения σ^I_zC и σ^II_zC определяются по указанным выше правилам. Коэффициенты α^I и α^II находятся из табл. 5.2 по значениям безразмерных параметров l_I/b_I, z/b_I и l_II/b_II, z/b_II, где l_I, b_I, l_II, b_II – размеры сторон соответствующих прямоугольников. При этом всегда принимается, что b£l.

Если точка М лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда σ_zM=σ^I_zC+σ^II_zC+σ^III_zC+σ^IV_zC. Наконец, если точка М лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой. Тогда, полагая, что напряжения в точке М, возникают от действия нагрузки, распределенной по площади прямоугольников I и II, необходимо вычесть напряжения от действия той же фиктивной нагрузки, распределенной по площади прямоугольников III и IV, т. е. действительное напряжение определится выражением σ_zM=σ^I_zC+σ^II_zC-σ^III_zC-σ^IV_zC.

Естественно, что и в этих случаях правила определения угловых напряжений и соответствующих им значений коэффициентов а будут те же, что и приведенные для первого варианта.

Методом угловых точек обычно пользуются для расчетов взаимного влияния фундаментов, расположенных в непосредственной близости друг от друга.

Влияние формы и площади фундамента в плане. Пользуясь формулой σ_zC=1/4αp; σ_zO=αp и данными табл. 5.2, можно построить эпюры нормальных напряжений σ_z по вертикальной оси, проходящей через центр прямоугольного фундамента. В качестве примера на рис. 5.11 в относительных координатах построены такие эпюры для случаев: 1 — квадратного фундамента при l=Ь; 2 – ленточного фундамента (l≥10b) шириной Ь;
3 – то же, шириной 2Ь. Легко заметить, что в случае пространственной задачи (кривая 1) напряжения с глубиной затухания значительно быстрее, чем для плоской задачи
(кривая 2). Увеличение ширины, а следовательно, и площади фундамента (кривая 3) приводит к еще более медленному затуханию напряжений с глубиной.

Это обстоятельство легко объяснить исходя из принципа суперпозиции. Представляя, например, ленточный фундамент как ряд квадратных фундаментов, установленных вплотную друг к другу, можно с помощью метода угловых точек учесть дополнительное влияние нагрузки, действующей на соседние фундаменты.

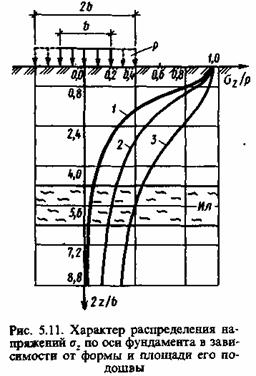Указанная закономерность имеет важное практическое значение. Если, например, в основании на некоторой глубине залегает слабый прослоек (ил на рис. 5.11), то можно подобрать такую форму и площадь фундамента, чтобы напряжения на кровле этого прослойка были меньше его несущей способности. В противном случае возможны чрезмерные осадки из-за выдавливания грунта слабого прослойка в стороны от оси фундамента.

Влияние неоднородности напластования грунтов. Приведенные выше решения справедливы для случая, когда основание сложено грунтами, близкими по деформационным показателям. Если же на некоторой глубине залегают существенно более
жесткие (например, скальные) грунты, возникает концентрация напряжений σ_z по оси фундамента, причем эффект концентрации напряжений тем больше, чем меньше относительная глубина залегания кровли этого слоя грунтов. Если же подстилающий слой грунта обладает значительно большей сжимаемостью, чем несущий, напротив, отмечается некоторое рассеивание (деконцентрация) напряжений σ_z.

На рис. 5.12 в качестве примера приведены также в относительных координатах эпюры напряжений σ_z по оси фундаментов.

Определение напряжений в массиве грунтов от действия собственного веса. Как указывалось ранее, напряжения, возникающие в массиве грунтов от действия сооружения, накладываются на поле начальных напряжений, сформировавшихся в массиве к моменту строительства. В общем случае начальные напряжения определяются не только силами гравитации (собственным весом грунта), но и изменением этих сил в процессе формирования массива (увеличение или уменьшение грунтовой толщи), тектоническими, сейсмическими воздействиями и рядом других факторов.

Начальное напряженное состояние массива грунта может также изменяться в период работ нулевого цикла: вследствие выемки грунта при разработке котлована, водопонижения, трамбования или укатки грунта и т. п. В этих случаях приходится говорить уже не о начальном, а видоизмененном — исходном напряженном состоянии основания, которое и взаимодействует далее с напряжениями, возникающими от сооружения.

Точное определение начального и исходного напряженного состояния массива грунтов представляет собой сложную задачу, связанную с необходимостью учета многих факторов. До настоящего времени пригодного для инженерных расчетов решения этой задачи еще не получено. Поэтому на практике обычно пользуются весьма упрощенным представлением о том, что природные напряжения в массиве грунтов определяются только силами гравитации, т. е. формируются под действием собственного веса. При этом считается, что все деформации массива от собственного веса грунта уже прекратились и напряжения полностью стабилизировались.

Тогда при горизонтальной поверхности массива грунтов напряжения на глубине z определяются выражениями

σ_z=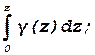σ_x=σ_y=ξσ_z;

τ_xy=τ_yz=τ_zx,

где y – удельный вес грунта; ξ – коэффициент бокового давления грунта в состоянии покоя.

Отсюда можно показать, что для однородного напластования при у(z)= const вертикальные напряжения от собственного веса грунта на глубине z от поверхности определяются формулой

σ_z=γz

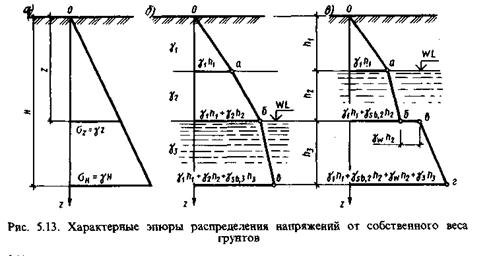
и эпюра природных напряжений будет иметь вид треугольника (рис. 5.13, а).

При неоднородном напластовании с горизонтальным залеганием слоев эта эпюра будет уже ограничиваться ломаной линией Оабв, где наклон каждого отрезка в пределах мощности слоя А, определяется значением удельного веса грунта этого слоя у_i (рис. 5.13, б). Важно отметить, что неоднородность напластования может вызываться не только наличием слоев с разными характеристиками, но и наличием в пределах толщи грунта уровня подземных вод (WL на рис. 5.13, б, в). В этом случае следует учесть уменьшение удельного веса грунта за счет взвешивающего действия воды на минеральные частицы:

γ_sb=(γ_s-γ_w)/(1+e),

где γ_sb – удельный вес грунта во взвешенном состоянии; γ_s – удельный вес частиц грунта; γ_w – удельный вес воды, принимаемый равным 10 кН/м³; е – коэффициент пористости грунта.

Если на некоторой глубине ниже уровня подземных вод залегает водоупорный слой (плотные глины или суглинки), то на его кровле необходимо учитывать также и давление от столба вышележащей воды, обозначенное на рис. 5.13, в как укЛ2. Тогда эпюра природного давления будет уже ограничиваться линией Оабвг.

Определив значения компонент вертикальных напряжений стг при любом напластовании грунтов и зная соответствующие значения коэффициентов бокового давления ξ, можно по формуле (5.20) найти значения компонент горизонтальных напряжений σ_x=σ_y.