Символьная обработка – основа обработки информации (данных) «Лиспа».
Fib_fast(N,FN,_).
Лекция 8. Язык программирования «Лисп»
Автор языка Лисп – профессор математики и философии Джон Мак-Карти, выдающийся ученый в области искусственного интеллекта. Он предложил проект языка Лисп, идеи которого возбудили не утихающие до наших дней дискуссии о сущности программирования. Сформулированная Джоном Мак-Каpти (1958) концепция символьной обработки информации восходит к идеям Чёрча и других видных математиков конца 20-ых годов предыдущего века. Выбирая лямбда-исчисление как основную модель, Мак-Карти предложил функции рассматривать как общее понятие, к которому могут быть сведены все другие понятия программирования. Знакомство с Лиспом - важная составляющая современного образования в области информатики. Лисп является ключом для изучения типовых задач системного программирования и искусственного интеллекта.
«Лисп» изначально поддерживает программирование в функциональном стиле. Его основа - выбор подходящей структуры данных и базового набора функций над выбранной структурой. Информационная обработка в языке Лисп отличается от стандартных подходов к программированию тремя важными особенностями:
- Природа данных
Любая информация представляется в форме символьных выражений. Система программирования над такими структурами обычно использует для их хранения всю доступную память, поэтому программист принципиально освобожден от заботы о распределении памяти под отдельные блоки данных.
- Самоописание обработки символьных выражений
Важная особенность программ на Лиспе - они строятся из рекурсивных функций, определения и вызовы которых, как и любая информация, формально могут обрабатываться как обычные данные, получаться в процессе вычислений как значения и преобразовываться как символьные выражения.
- Подобие машинным языкам
Система программирования на «Лиспе» допускает, что программа может интерпретировать и (или) компилировать программы, представленные в виде символьных выражений. Это сближает программирование на Лиспе с методами низкоуровневого программирования и отличает от традиционной методики применения языков высокого уровня.
Любые структуры данных строятся из более простых составляющих, простейшие из которых – элементарные данные. В Лиспе элементарные данные называют атомами. Для начала примем, что атом – это последовательность из букв и цифр, начинающаяся с буквы.
Одинаково выглядящие атомы не различимы по своим свойствам. Термин "атом" выбран по аналогии с химическими атомами, строение которых – предмет другой науки. Согласно этой аналогии атом может иметь достаточно сложное строение, но атом не предназначен для разбора на части базовыми средствами языка.
Более сложные данные в «Лиспе» выстраиваются из одинаково устроенных бинарных узлов, содержащих пары объектов произвольного вида. Каждый бинарный узел соответствует минимальному блоку памяти, выделяемому системой программирования при организации и обработке структур данных. Выделение блока памяти и размещение в нем пары данных выполняет функция CONS (от слова consolidation), а извлечение левой и правой частей из блока выполняют функции CAR и CDR соответственно (" content of address part of register ", " content of decrement part of register ").
Типичная форма записи символьных выражений называется списочной записью (list-notation). Элементы списка могут быть любой природы.
Список – это перечень произвольного числа элементов, разделенных пробелами, заключенный в круглые скобки.
Примеры записи на языке «Лисп»:
| (CONS 'ATOM ' X) |
| (CAR '(ATOM. X) |
| (CDR '(ATOM. X) |
| Здесь: 'ATOM и ' X -аргументы; CONS - функция. Результаты выполнения команд: |
1) (АТОМ,Х); 2) АТОМ; 3) Х
По соглашению атом Nil выполняет роль пустого списка. Бинарный узел, содержащий пару атомов ATOM и Nil, рассматривается как одноэлементный список (ATOM):

или для наглядности:

Если вместо атома "ATOM" подставлять произвольные атомы, а вместо "Nil" - произвольные списки, затем вместо атомов - построенные списки и так далее, то мы получим множество всех возможных списков. Можно уточнить, что список - это заключенная в скобки последовательность из разделенных пробелами атомов или списков. (C)
Любой список может быть построен из пустого списка и атомов с помощью CONS и любая его часть может быть выделена с помощью подходящей композиции CAR-CDR.
CONS - Функция, которая строит списки из бинарных узлов, заполняя их парами объектов, являющихся значениями пары ее аргументов. Первый аргумент произвольного вида размещается в левой части бинарного узла, а второй, являющийся списком, - в правой.
CAR – Функция, обеспечивающая доступ к первому элементу списка - его "голове".
CDR – Функция, укорачивающая список на один элемент. Обеспечивает доступ к "хвосту" списка, т.е. к остатку списка после удаления его головы.
ATOM - Функция, различающая составные и атомарные объекты. На атомах ее значение "истина", а на более сложных структурах данных – "ложь".
EQ – Функция, которая проверяет атомарные объекты на равенство.
Точечная нотация
При реализации Лиспа в качестве единой универсальной базовой структуры для конструирования символьных выражений использовалась так называемая "точечная нотация" (dot-nоtation), согласно которой левая и правая части бинарного узла равноправны и могут хранить данные любой природы.
Бинарный узел, содержащий пару атомов ATOM1 и ATOM2,
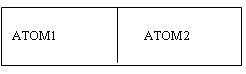
можно представить как запись вида:
(ATOM1. ATOM2)
Если вместо атомов "ATOM1", "ATOM2" рекурсивно подставлять произвольные атомы, затем построенные из них пары и так далее, то мы получим множество всех возможных составных символьных выражений – S-выражений.
S-выражение - это или атом или заключенная в скобки пара из двух S-выражений, разделенных точкой.
Упражнения 8.1-8.3: Нарисуйте диаграммы для списков вида:
((A B) C) ((A B) (D C)) ((A B)(D(C E)))Все сложные данные создаются из одинаково устроенных блоков - бинарных узлов, содержащих пары объектов произвольного вида. Каждый бинарный узел соответствует минимальному блоку памяти.
Списки – это подмножество S-выражений, движение вправо по которым завершается атомом Nil. (C. (A. B))
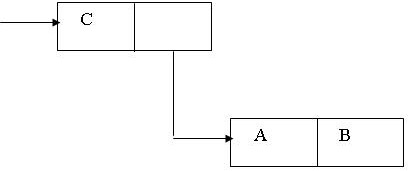
(A. B)

Любое S-выражение может быть построено из атомов с помощью CONS и любая его часть может быть выделена с помощью CAR-CDR.
Упражнение 8.4. Нарисуйте диаграммы для следующих S-выражений:
((A. B). C)
((A. B). (D. C))
((A. B). (D. (C. E)))
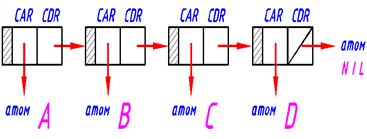
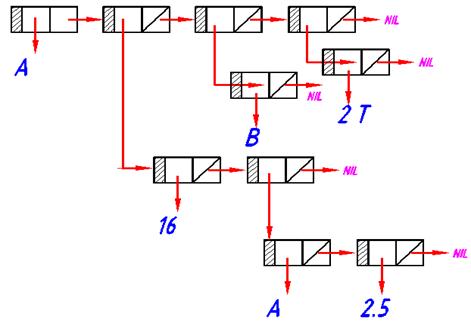
Рис.8.1 Представление простого списка (ABCD) и списка с подсписками
(A (16 (A 2.5))(B)(21))
| Таблица 8.1. Соответствие списков и равнозначных им S-выражений | |
| List-notation - списочная запись объекта | Dot-notation - точечная запись того же объекта |
| (A B C) | (A. (B. (C. Nil))) |
| ((A B) C) | ((A. (B. Nil)). (C. Nil)) |
| (A B (C E)) | (A. (B. ((C. (E. Nil)). Nil))) |
| (A) | (A. Nil) |
| ((A)) | ((A. Nil). Nil |
| (A (B. C)) | (A. ((B. C). Nil)) |
| (()) | (Nil. Nil) |
| (A B. C) | (A. (B. C)) |
Для многошагового доступа к отдельным элементам такой структуры удобно пользоваться мнемоническими обозначениями композиций из многократных CAR-CDR. Имена таких композиций устроены как цепочки из "a" или "d", задающие маршрут движения из шагов CAR и CDR соответственно, расположенный между "c" и "r". Указанные таким способом CAR-CDR исполняются с ближайшего к аргументу шага, т.е. в порядке, обратном записи.
| Таблица 8.2. Примеры многошагового доступа к элементам структуры. | ||
| Композиции CAR-CDR | Вычисляются в порядке, обратном записи: | |
| CAAR | ((A) B C) | A |
| CADR | (A B C) | B - CDR, затем CAR |
| CADDR | (A B C) | C - (дважды CDR), затем CAR |
| CADADR | (A (B C) D) | C - два раза:(CDR, затем CAR) |
Упражнение 8.5. Посмотрите, что делает Лисп-система с ниже приведенными выражениями, сравнивая результаты с данными из таблицы 8.1:
(cAAr '((A) B C))
(cADr '(A B C))
(cADDr '(A B C))
(cADADr '(A (B C) D))
Выводы:
- Список – это перечень произвольного числа элементов, разделенных пробелами, заключенный в круглые скобки.
- Элементы списка могут быть любой природы.
- S-выражение - это или атом или заключенная в скобки пара из двух S-выражений, разделенных точкой. Список – частный случай S-выражения.
- Любое S-выражение может быть построено из атомов с помощью CONS и любая его часть может быть выделена с помощью CAR-CDR.
- Для изображения S-выражений используют различные нотации: графическую, точечную и списочную.
- Базис Лиспа содержит элементарные функции CAR, CDR, CONS, EQ, ATOM.
Базис элементарного Лиспа образуют пять функций над S-выражениями CAR, CDR, CONS, ATOM, EQ и четыре специальных функции, обеспечивающие управление программами и процессами и конструирование функциональных объектов QUOTE, COND, LAMBDA, DEFUN.
Далее мы построим определение универсальной функции EVAL, позволяющее вычислять значения выражений, представленных в виде списков, - правило интерпретации выражений.
Формально для перехода к практике нужна несколько большая определенность по механизмам исполнения программ, представленных S-выражениями:
- аргументы функций, как правило вычисляются в порядке их перечисления,
- композиции функций выполняются в порядке от самой внутренней функции наружу до самой внешней,
- представление функции анализируется до того, как начинают вычисляться аргументы, т.к. в случае специальных функций аргументы можно не вычислять,
- при вычислении лямбда-выражений связи между именами переменных и их значениями, а также между именами функций и их определениями, накапливаются в так называемом ассоциативном списке, пополняемом при вызове функции и освобождаемом при выходе из функции.
| Таблица 8.3. Clisp: Функции, строящие функциональные объекты. | |
| (Declare Спецификации) | Специфицирует переменные – dynamic-extent, ftype, ignorable, ignore, inline, optimize, special, type |
| (Defmacro Название Параметры Определение) | Глобальное опреление макроса |
| (Defun Название Параметры Форма) | Определение функции |
| (Function Название) | #’ – выдает названную функцию |
| (Lambda Параметры Определение) | Конструирует безымянную функцию |
Выводы:
- Основные понятия, возникающие при написании программ – это переменные, константы, выражения, ветвления, вызовов функций и определения. Все они представимы с помощью S-выражений.
- Связанную переменную можно объявить специальной функцией Lambda, а значение она получит при вызове функции.
- Представления функции могут вычисляться и передаваться как параметры или результаты других функций.
- Специальные функции не требуют предварительной обработки параметров.
- Базис элементарного Лиспа образуют пять функций над S-выражениями CAR, CDR, CONS, ATOM, EQ и четыре специальных функции, обеспечивающие управление программами и процессами и конструирование функциональных объектов QUOTE, COND, LAMBDA.
Синтаксис данных
в Лиспе сводится к правилам представления атомов и S-выражений.
<атом>::= <БУКВА> <конец_атома><конец_атома>::= <пусто> | <БУКВА> <конец_атома> | <цифра> <конец_атома>В Лиспе атомы - это мельчайшие частицы. Их разложение по литерам обычно не имеет смысла.
<S-выражение>::= <атом> | (<S-выражение>. <S-выражение>); пара | (<S-выражение>...); списокПо этому правилу S-выражения - это или атомы, или бинарные узлы из пары S-выражений, или списки из S-выражений.
/Три точки означают, что допустимо любое число вхождений предшествующего вида объектов, включая ни одного./
Символ ";" - начало комментария до конца строки.
Т.о. "()" есть допустимое S-выражение. Оно в языке Лисп по соглашению эквивалентно атому Nil.
Базовая система кодирования данных - точечная нотация, хотя на уровне текста запись в виде списков удобнее. Любой список можно представить точечной нотацией:
() = Nil (a. Nil) = (a) - - - (a1. (... (aK. Nil)...)) = (a1... aK)Такая единая структура данных оказалась вполне достаточной для представления сколь угодно сложных программ в виде двоичных деревьев. Дальнейшее определение языка Лиспа можно рассматривать как восходящий процесс генерации семантического каркаса, по ключевым позициям которого распределены семантические действия по обработке программ.
Другие правила представления данных нужны лишь при расширении и специализации лексики языка (числа, строки, имена особого вида и т.п.). Они не влияют ни на общий синтаксис языка, ни на строй его понятий, а лишь характеризуют разнообразие сферы его конкретных приложений.
Синтаксис программ в Лиспе внешне не отличается от синтаксиса данных. Просто выделяем вычислимые выражения (формы), т.е. данные, приспособленные к вычислению. Внешне это выглядит как объявление объектов, заранее известных в языке, и представление разных форм, вычисление которых обладает определенной спецификой.
Выполнение программы на Лиспе устроено как интерпретация данных, представляющих выражения, имеющие значение. Ниже приведены синтаксические правила для обычных конструкций, таких как идентификаторы, переменные, константы, аргументы, формы и функции.
<идентификатор>::= <атом> Идентификаторы - это атомы, используемые при именовании неоднократно используемых объектов программы - функций и переменных. Предполагается, что объекты размещаются в памяти так, что по идентификатору их можно найти.<форма>::= <константа> | <переменная> | (COND (<форма> <форма>) (<форма> <форма>)...) | (<функция> <аргумент>... >) <константа>::= (QOUTE <S-выражение>) | '<S-выражение> <переменная>::= <идентификатор>Переменная - это идентификатор, имеющий многократно используемое значение, ранее вычисленное в подходящем контексте. Подразумевается, что одна и та же переменная в разных контекстах может иметь разные значения.
Форма - это выражение, которое может быть вычислено. Формами являются переменные и списки, начинающиеся с QUOTE, COND или представления некоторой функции.
<аргумент>::= <форма>Если форма представляет собой константу, то нет необходимости в вычислениях, независимо от вида константы. Константные значения, могут быть любой сложности, включая вычислимые выражения, но в данный момент они не вычисляются. Константы изображаются с помощью специальной функции QUOTE, блокирующей вычисление. Представление констант с помощью QOUTE устанавливает границу, далее которой вычисление не идет. Использование апострофа (') - просто сокращенное обозначение для удобства набора текста. Константные значения аргументов характерны при тестировании и демонстрации программ.
Если форма представляет собой переменную, то ее значением должно быть S-выражение, связанное с этой переменной до момента вычисления формы. Следовательно где-то хранится некая таблица, по которой, зная имя переменной, можно найти ее значение.
Третье правило гласит, что можно написать функцию, затем перечислить ее аргументы и все это как общий список заключить в скобки.
Аргументы представляются формами. Это означает, что допустимы композиции функций. Обычно аргументы вычисляются в порядке вхождения в список аргументов.
Последнее правило задает формат условного выражения. Согласно этому формату условное выражение строится из размещенных в двухэлементном списке синтаксически различимых позиций для условий и обычных форм. Двухэлементные списки из определения условного выражения рассматриваются как представление предиката и соответствующего ему S-выражения. Значение условного выражения определяется перебором предикатов по порядку, пока не найдется форма, значение которой отлично от Nil, что означает логическое значение "истина". Строго говоря, такая форма должна найтись непременно. Тогда вычисляется S-выражение, размещенное вторым элементом этого же двухэлементного списка. Остальные предикаты и формы условного выражения не вычисляют (логика Мак-Карти), их формальная корректность или определенность не влияют на существование результата.
(COND (p1 e1) (p2 e2)... (pk ek)) |______|________|__________ предикаты для выбора ветви |______|____ ___|__________ ветви условного выраженияКаждый предикат pi или ветвь ei может быть любой формы: переменная, константа, вызов функции, композиция функций, условное выражение.
Обычное условное выражение (if Predicate Then Else) или (если Predicate то Then иначе Else) может быть представлено с помощью функции COND следующим образом:
(COND (Predicate Then)(T Else))Разница между предикатами и обычными формами заключается лишь в трактовке их результатов. Любая форма может выполнить роль предиката.
<функция>::= <название> | (LAMBDA <список_переменных> <форма>) | (DEFUN <название> <список_переменных> <форма>) <список_переменных>::= (<переменная>...) <название> = <идентификатор>Название функции - это идентификатор, определение которого хранится в памяти, но оно может не подвергаться влиянию контекста вычислений.
Таким образом, функция - это или название, или список, начинающийся с LAMBDA или DEFUN.
Функция может быть представлена просто именем. В таком случае ее смысл должен быть заранее известен. Например, встроенные функции CAR, CDR и т.д.
Функция может быть введена с помощью лямбда-конструктора, устанавливающего соответствие между аргументами функции и связанными переменными, входящими в тело ее определения (в определяющей ее форме). Форма из определения функции может включать переменные, не включенные в лямбда-список, - так называемые свободные переменные. Их значения должны устанавливаться на более внешнем уровне. Если функция рекурсивна, то следует объявить ее имя с помощью специальной функции DEFUN.
Общий механизм вычисления форм будет позднее определен как универсальная функция EVAL, а сейчас запрограммируем ряд вспомогательных функций, полезных при обработке S-выражений. Некоторые из них пригодятся при определении интерпретатора.
Начнем с общих методов обработки S-выражений.
AMONG – проверка входит ли заданный атом в данное S-выражение.
(DEFUN among (x y) (COND ((ATOM y) (EQ x y)) ((among x (CAR y)) (QUOTE T)) ((QUOTE T) (among x (CDR y))))) (among 'A '(B. A))EQUAL - предикат, проверяющий равенство двух S-выражений. Его значение "истина" для идентичных аргументов и "ложь" для различных. (Элементарный предикат EQ строго определен только для атомов.) Определение EQUAL иллюстрирует условное выражение внутри условного выражения (двухуровневое условное выражение и двунаправленная рекурсия)
(DEFUN equal (x y) (COND ((ATOM x) (COND ((ATOM y) (EQ x y)) ((QUOTE T) (QUOTE NIL)))) ((equal (CAR x)(CAR y)) (equal (CDR x)(CDR y))) ((QUOTE T) (QUOTE NIL)))) (equal '(A B) '(A. B))(equal '(A B) '(A. (B. Nil)))При желании можно дать название этой функции по-русски:
(DEFUN равно_ли (x y) (equal x y)) 2014-02-12
2014-02-12 787
787








