Пример 8

Изучается зависимость себестоимости единицы изделия (y, тыс. руб.) от величины выпуска продукции (x, тыс. шт.) по группам предприятий за отчетный период. Экономист обследовал 5 предприятий и получил результаты, представленные в таблице.

x
y	1,9	1,7	1,8	1,6	1,4

Найти

а) выборочное уравнение линейной регрессии;

б) коэффициенты корреляции и детерминации;

в) ожидаемое значение себестоимости y при выпуске продукции x = 5,5 тыс.шт.;

г) проверить гипотезу о наличии линейной взаимосвязи между переменными с доверительной вероятностью 95% на основе оценки коэффициента корреляции;

д) проверить гипотезу о наличии линейной взаимосвязи между переменными с доверительной вероятностью 95% на основе оценки показателя наклона линейной регрессии.

Решение.

а) Найдем уравнение линейной регрессии 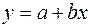. Используя функции Excel: a = ОТРЕЗОК(изв_значение_y; изв_значение_x) = 2,12;

b = НАКЛОН(изв_значение_y; изв_значение_x) = ¾ 0,11.

Уравнение имеет вид .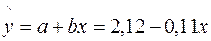

б) Найдем коэффициент корреляции Пирсона с помощью функции ПИРСОН(массив 1; массив 2), получаем r = ¾ 0,904. Так как получили значение, близкое к 1, следовательно, связь между x и y близка к линейной.

Найдем коэффициент детерминации с помощью функции КВПИРСОН(изв_значение_y; изв_значение_x), получаем 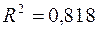. Это значение показывает, что 82% вариации переменной y объясняется переменной x.

в) Найдем ожидаемое значение себестоимости y при выпуске продукции x = 5,5 тыс.шт. с помощью функции ПРЕДСКАЗ(x; изв_значение_y; изв_значение_x), получаем 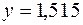тыс. руб.

г) проверим гипотезу о наличии линейной взаимосвязи между переменными с доверительной вероятностью 95% на основе оценки коэффициента корреляции. Выдвигаем гипотезы:

H₀: 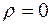, то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности;

H₁: 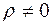то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности.

Доверительная вероятность p = 0,95, следовательно 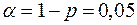. Объем n = 5. Граничные точки 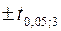определяем с помощью функции СТЬЮДРАСПОБР(0,05; 3) и получаем 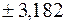. Статистика вычисляется по формуле .

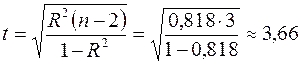Отметим значения на числовой оси

Отклоняем гипотезу H₀ и принимаем гипотезу H₁ на уровне значимости 5%. Между переменными есть линейная взаимосвязь.

д) проверим гипотезу о наличии линейной взаимосвязи между переменными с доверительной вероятностью 95% на основе оценки показателя наклона линейной регрессии. Выдвигаем гипотезы:

H₀: 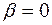, то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности;

H₁: 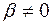то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности.

Доверительная вероятность p = 0,95, следовательно 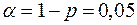. Объем 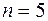. Граничные точки 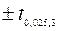определяем с помощью функции СТЬЮДРАСПОБР(0,05; 3) и получаем .

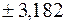Вычисляем стандартную ошибку S с помощью функции СТОШYX(изв_значение_y; изв_значение_x). Получаем 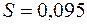. Далее вычисляем 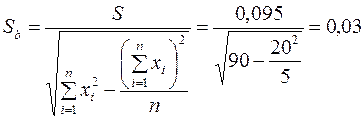. Вычисляем статистику по формуле .

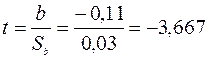Отметим значения на числовой оси

Отклоняем гипотезу H₀ и принимаем гипотезу H₁ на уровне значимости 5%. Между переменными есть линейная взаимосвязь.