Испытание гипотезы для оценки линейности связи

Показатель наличия линейной связи в генеральной совокупности ¾ это коэффициент корреляции. Для генеральной совокупности он равен 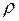. Нам это значение неизвестно. По данным выборки мы получаем оценку для 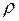¾ выборочный коэффициент корреляции r ¾ и на основании r проводим испытание гипотезы о наличии линейной связи между переменными x и y в генеральной совокупности. Наш вывод зависит от объема выборки. Чем больше объем выборки, тем надежнее результат.

Выдвигаются следующие гипотезы:

H₀: 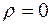, то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности;

H₁: 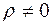то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности.

Задается доверительная вероятность p, следовательно 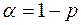. Объем равен n. Граничные точки 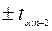определяются с помощью функции СТЬЮДРАСПОБР(a; n ¾ 2). Статистика вычисляется по формуле .

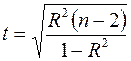В случае парной линейной регрессии коэффициент 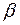аналогичен коэффициенту корреляции 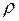. Поэтому можно проводить испытание гипотезы на основе показателя наклона линейной регрессии .

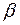Выдвигаются следующие гипотезы:

H₀: 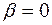, то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности;

H₁: 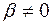то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности.

Задается доверительная вероятность p, следовательно 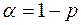. Объем равен n. Граничные точки 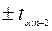определяются с помощью функции СТЬЮДРАСПОБР(a; n ¾ 2). Статистика вычисляется по формул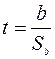е , где 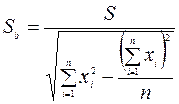, 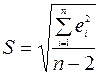. Разница 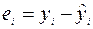называется ошибкой (остатком, отклонением). Величина S называется стандартной ошибкой. Для вычисления S можно воспользоваться функцией СТОШYX(изв_значение_y; изв_значение_x).