Выборочной ковариацией двух переменных х, у называется средняя величина произведения отклонений этих переменных от своих средних, т. е.
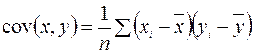 или
или 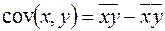
где 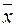 ,
, 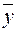 — выборочные средние переменных х, у.
— выборочные средние переменных х, у.
Ковариацию можно вычислить с помощью функции Excel КОВАР(массив1; массив2), где Массив 1 и 2 ¾ это значения x и y.
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
Пусть данные наблюдений переменных х, у представлены в виде точечного графика – диаграммы рассеяния наблюдений
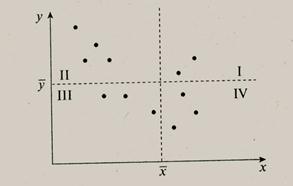
Точка 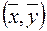 на диаграмме является центром рассеяния переменных х, у.
на диаграмме является центром рассеяния переменных х, у.
Вертикальная и горизонтальная прямые, проведенные через точку 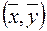 , разделяют диаграмму рассеяния на четыре области.
, разделяют диаграмму рассеяния на четыре области.
Наблюдения в областях I, III дают положительный вклад в ковариацию, а в областях II, IV — отрицательный.
Если положительные вклады преобладают над отрицательными, то ковариация будет положительной, в противном случае она будет отрицательной. Положительной ковариации отвечает положительная связь, а отрицательной — отрицательная.
При положительной (прямой) связи с увеличением одной переменной другая переменная в среднем также увеличивается, и наоборот при отрицательной (обратной) связи.
Заметим, что 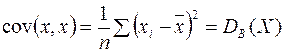
Свойства ковариации:
1) 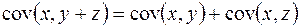 ;
;
2) 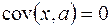 , где а – константа;
, где а – константа;
3) 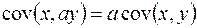 , где а – константа;
, где а – константа;
4) 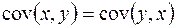
Пусть выборка извлечена из нормальной генеральной совокупности и отражает ее свойства.
Если случайные величины X, У независимы, то ковариация равна нулюи выборочные точки на диаграмме рассеяния наблюдений можно заключить в окружность с центром в точке 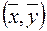 .
.
Если X, У зависимы, то ковариация отлична от нуляи выборочные точки можно заключить в эллипс с центром в точке 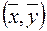 , при этом положение большей полуоси эллипса будет указывать направление связи (положительная или отрицательная).
, при этом положение большей полуоси эллипса будет указывать направление связи (положительная или отрицательная).
Более точной мерой зависимости между величинами является коэффициент корреляции.
Выборочный коэффициент корреляции определяется выражением
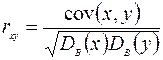 ,
,
он является безразмерной величиной и показывает степень линейной связи двух переменных.
Коэффициент корреляции можно вычислить с помощью функции Excel КОРРЕЛ(массив1; массив2), где Массив 1 и 2 ¾ это значения x и y.
Свойства коэффициента корреляции:
1) 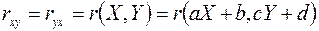 ;
;
2) 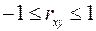 ;
;
3) если 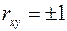 , то X и Y точно связаны линейной функциональной зависимостью;
, то X и Y точно связаны линейной функциональной зависимостью;
4) если 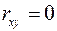 , то между X и Y нет линейной корреляционной зависимости, но это не исключает существования другого вида зависимости;
, то между X и Y нет линейной корреляционной зависимости, но это не исключает существования другого вида зависимости;
5) если 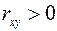 , то имеет место прямая корреляционная зависимость;
, то имеет место прямая корреляционная зависимость;
6) если 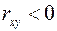 , то имеет место обратная корреляционная зависимость.
, то имеет место обратная корреляционная зависимость.
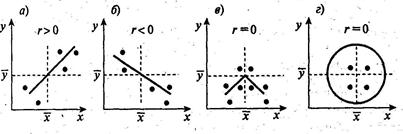
На рисунках отражен геометрический смысл коэффициента корреляции. На рисунках а и б случайные величины X, У коррелированы (r > 0 или r < 0), на рисунках в и г — некоррелированы (r = 0). Если r = 0, случайные величины могут быть как зависимыми (см. рис. в), так и независимыми(см. рис. г).
Выборочный коэффициент корреляции является случайной величиной.
Проверка гипотезы о корреляции случайных величин. Пусть по данным выборки объема п получен выборочный коэффициент корреляции r ¹ 0. Требуется проверить гипотезу о равенстве нулю истинного значения коэффициента корреляции r, т.е,
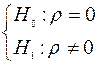
Статистика определяется по формуле
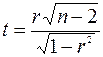 .
.
Граничная точка 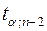 определяется с помощью функции пакета Exel: СТЬЮДРАСПОБР(1− p; n− 2).
определяется с помощью функции пакета Exel: СТЬЮДРАСПОБР(1− p; n− 2).
 2014-02-12
2014-02-12 3734
3734
