Упорядоченность

ОТНОШЕНИЕ ПОРЯДКА

Отношение порядка обладает свойствами рефлексивности, транзитивности и антисимметричности. Его принято обозначать символом £. Запись х £ у означает, что пара (х, у) принадлежит множеству 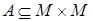, являющемуся отноше­нием порядка в множестве М, причем х предшествует у (или у следует за х). В принятых обозначениях свойства отношения порядка запишутся следующим образом:

1) х £ у (рефлексивность);

2) х £ у Ù у £ z Þ х £ z (транзитивность);

3) х £ у Ù у £ х Þ х=у (антисимметричность).

Множество, на котором определено отношение порядка, назы­вают упорядоченным, и говорят, что порядок введен этим отношением. Множество совершенно (линейно, просто), упорядочено, если для любых двух его элементов имеет место, по крайней мере, х £ у или у £ х (например, множество нату­ральных или действительных чисел с естественным отношением порядка).

В общем случае может оказаться, что для некоторых пар (х, у) ни одно из соотношений х £ у и у £ х не имеет места (такие эле­менты называют несравнимыми). Тогда говорят, что множество частично упорядочено. Типичными примерами частичного порядка являются включение, отношение «быть делителем» и т. п. Так, отно­шение включения на множестве подмножеств некоторого универсу­ма рефлексивно, транзитивно и антисимметрично,но среди всевозможных подмножеств имеются такие, что ни одно из соотношений Х Í Y и Y Í Х для них не имеет места. Аналогично не все пары элементов из множества целых чисел находятся в отно­шении «быть делителем».