Матрица и граф отношения эквивалентности

Элементы, принадлежащие некоторому классу эквивалентности, попарно эквивалентны между собой, а их сечения совпадают. Следовательно, столбцы матрицы отношения эквивалентности для элементов одного класса одинаковы и содержат единицы во всех строках, которые соответствуют этим элементам. Так как классы эквивалентности не пересекаются, то в столбцах различных классов не будет единиц в одинаковых строках.

Расположим элементы множества так, чтобы в каждом классе эквивалентности принадлежащие ему элементы стояли рядом. Тогда единичные элементы матрицы отношения эквивалентности образуют непересекающиеся квадраты, диагонали которых располагаются по главной диагонали матрицы. Например, для разбиения на классы эквивалентности 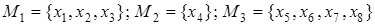имеем:

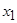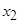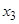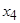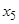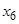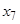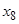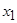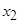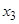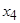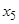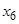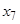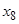На рис. 4.1 изображен граф отношения эквивалентности, матрица которого приведена выше. Каждому классу эквивалентности соответствует отдельная часть графа, которая представляет собой полный направленный граф на множестве ее вершин.

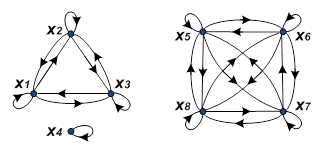рис.4.1. Граф отношения эквивалентности

4.5. Разбиение и отображение. Разбиение множества на классы можно связать с отображением f: Х ® У, ставящим каждому элементу из Х в соответствие один и только один элемент из У (рис. 4.2).

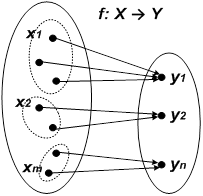рис.4.2. Отображение, порождающее отношение эквивалентности

Собирая в один класс все те элементы из X, образы которых в У совпадают, приходим к некоторому разбиению на непересекающиеся подмножества 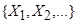. Каждое подмножество 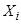характеризуется соответствующим ему образом 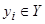и является классом эквивалентности.

Обратно, если задана некоторая совокупность классов эквивалентности 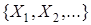множества X, то каждому элементу хÎХ можно поставить в соответствие тот класс X_i, к которому принадлежит х. В результате получаем отображение множества Х на множество классов 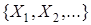.Итак, любое отображение f: Х ® У порождает отношение эквивалентности на множестве X, причем 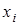~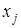, если и только если 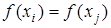. Образы 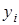классов эквивалентности 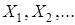могут служить эталонами и образуют в совокупности систему представителей.