Квазипорядок

Если отображение 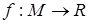не инъективно, т.е. два различных объекта х и у из М могут иметь равные веса 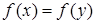, то отношение между ними не является антисимметричным и, следовательно, не удовлетворяет определению порядка. В то же время, как показано ранее, с отображением можно связать разбиение множества М на классы эквивалентности. Каждый из них объединяет различные эле­менты из М с равными весами, причем этот вес служит представи­телем соответствующего класса.

Теперь можно говорить об упорядочении совокупности классов эквивалентности некоторого множества М по их представителям. Так как система представителей не содержит одинаковых элементов (в противном случае соответствующие им классы объединились бы в общий класс эквива­лентности), то на этой системе как на множестве можно определить строгий порядок. Такое упорядочение отождествляет элементы множества М, принадлежащие к одному и тому же классу эквива­лентности, и определяет на этом множестве квазипорядок (псевдпорядок). Говорят также, что строгий порядок на множестве классов эквивалентности множества М индуцируется квази­порядком.

Квазипорядок удовлетворяет условиям рефлексивности и тран­зитивности, Он является обобщением эквивалентности (в определение не входит свойство симметричности) и нестрогого порядка (не обязательно свойство антисимметричности). Отношение, явля­ющееся одновременно эквивалентностью и нестрогим порядком, есть тождественное равенство. Можно также показать, что если А - квазипорядок, то 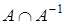- эквивалентность. Совершенный ква­зипорядок индуцирует и совершенно строгий порядок на мно­жестве классов эквивалентности. Классы эквивалентности множества М с квазипорядком, представляющие собой такие множества, где весо­вая функция принимает фиксированные значения, обычно называ­ются областями уровня.