Основные понятия. Глава 2. Алгебраические действия общего типа

Глава 2. Алгебраические действия общего типа

Пусть А – непустое множество и n ³1. Тогда n – арным действием (или n –местной операцией) на множестве А называется отображение некоторого подмножества декартова произведения 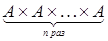в А.

Обозначение: φⁿ: Аⁿ ® А.

Могут рассматриваться также нуль–арные действия (операции), которые по определению отмечают некоторый элемент из А. При n = 1 операция называется унарной, например, а ^–1. При n = 2 – бинарной, например a + b. При n = 3 – тернарной, например, нахождение центра тяжести векторов на плоскости f (x, y, z)=(x + y + z)/3. И т.д.. Чаще всего рассматриваются бинарные операции, для которых по определению некоторым парам элементов x, y Î A (или каждой паре элементов в частном случае), взятых в определенном порядке, сопоставляется третий элемент z Î A, называемый результатом выполнения операции над операндами x и y.

Отметим, что действие всегда задается на определенном множестве, поэтому в этом смысле сложение на множестве натуральных чисел и сложение на множестве рациональных чисел – разные действия, т.к. отличаются множествами, на которых они заданы.

На одном и том же множестве может быть задано несколько действий.

Множество всех действий (операций), заданных на множестве А, называется сигнатурой А, т.е. Ω(А)= { φ ˚, φ ¹, φ ²,…} – сигнатура А. Множество А вместе с заданной на нем сигнатурой, возможно пустой, называется универсальной алгеброй или алгебраической системой и обозначается (А, Ω).

Для обозначения бинарного действия могут употребляться следующие формы записи: z = φ (x, y) или z = x ° y, если z Î A – результат некоторого действия над x и y Î A, а «°» – обозначение действия (традиционно для обозначения действия используются знаки: +, –, ´,:, /, *, ×, Å и т.д., при этом, используемое обозначение не обязательно показывает совпадение действия с известным элементарным действием). Запись вида z = x * y или z = x × y, или z = xy называется мультипликативной, а z = x + y – аддитивной. При этом используется обычная терминология: операнды называются сомножителями (слагаемыми), а результат – произведением (суммой), хотя само действие может не иметь ничего общего с обычным умножением или сложением чисел.

§ 2.2. Способы задания действий

1) Указать закон (формулу), выделяющий те пары элементов из А, для которых определен результат, и то, как строится результат для каждой такой пары, т.е. z = φ (x, y).

2) Непосредственно перечислить все результаты действия. Наиболее удобным представлением в таком случае является так называемая таблица Кэли (таблица умножения при мультипликативной записи). Слева и сверху этой прямоугольной таблицы выписываются все элементы множества, а на пересечении строк и столбцов – результат действия над соответствующими элементами или знак «–», если результат не определен. Теоретически такая таблица может быть построена для любого множества, конечного и даже бесконечного, практически рассматриваются только конечные множества и конечные таблицы.

Пусть на множестве А задано действие «°», и В Ì А. Тогда В называется замкнутым по отношению к действию, если для любых элементов x, y Î В Þ x ° y Î В.

Например, рассмотрим действия сложения и вычитания на множестве целых чисел, т.е. (ℤ, +) и (ℤ, –), и множество натуральных чисел ℕÌ ℤ. Тогда ℕ замкнуто по отношению к сложению и не замкнуто по отношению к вычитанию, поскольку не для любых пар натуральных чисел x и y результат (x ‑ y)Îℕ.

Пусть имеются множества с действиями: (А, ○) и (В, ◊). Множества А и В называются изоморфными относительно действий «○» и «◊», если существует биективное отображение f: А ® В такое, что для любых элементов а ₁ и а ₂ из А и соответствующих им элементов b ₁ и b ₂ из В, где b ₁= f (а ₁) и b ₂= f (а ₂), результат (а ₁○ а ₂) определен, т.е. Î А, тогда и только тогда, когда результат (b ₁◊ b ₂)Î В и при этом f (а ₁○ а ₂)= (b ₁◊ b ₂), т.е. результаты также соответствуют друг другу.

Смысл и значение понятия изоморфизма заключаются в том, что изоморфные множества с действиями являются одинаковыми относительно этих действий. Если в таблице Кэли одного из них элементы расположены в том же порядке, в каком расположены соответствующие им элементы второго, то таблицы Кэли обоих множеств окажутся совпадающими с точностью до обозначения элементов. Это означает, что действия в изоморфных множествах, по–существу, совершенно одинаковы.

Примеры:

1) А ={ 2, 3, 4, 5 } и В ={ 2, 4, 5, 10 }. Рассмотрим (А, +) и (В, ´) со следующими таблицами Кэли:

+

´

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

Существует биекция f: А ® В, где f ={ (2,2); (3,5); (4,4); (5,10) } и f (а₁+ а ₂) = f (а ₁) ´ f (а ₂) для любых элементов а ₁ и а ₂ из А, т.о. (А, +) изоморфно (В, ´) относительно заданных на них действий.

2) Рассмотрим множество натуральных чисел со сложением: (ℕ, +) и множество всех отрицательных четных целых чисел со сложением: (М, +), где М ={ x: x Îℤ.^<0 и x mod 2=0 }. Покажем, что они изоморфны относительно действий. Действительно, биекция f:ℕ ® М, заданная законом f (x)= ‑2 x, устанавливает этот изоморфизм. Т.к. для любых двух натуральных чисел x и y Þ f (x + y)= f (x)+ f (y), поскольку –2(x + y)=(–2 x)+(–2 y).

3) Рассмотрим множество положительных вещественных чисел с умножением (ℝ^>0, ´) и множество всех вещественных чисел со сложением (ℝ, +). Тогда изоморфизм устанавливается законом f (x)= ln (x), т.к. по свойствам логарифма ln (x ´ y)= ln (x)+ ln (y) для любых x, y Îℝ^>0.

4) Рассмотрим (ℕ, +) и (S, ´), где S ={ 2¹, 2², 2³, 2⁴, … }. Множества изоморфны относительно действий, т.к. для любых пар натуральных чисел x, y и соответствующих им 2 ^x и 2 ^y Î S Þ 2 ^{x + y} =2 ^x ´2 ^y.

5) (ℕ, +) неизоморфно (ℤ, +), т.к. в множестве целых чисел имеется элемент х =0, для которого выполняется х + х = х. В множестве натуральных чисел элементов с таким свойством нет.

Ввиду одинаковости действий для изоморфных множеств (в рассмотренном выше смысле) можно отвлечься от природы элементов, составляющих эти множества, и рассматривать их как одну алгебраическую систему, изучая сами действия и их свойства.

Замечания:

1. Свойства действий при изоморфизме сохраняются. Т.е. если действие «○» в множестве А было дистрибутивным, то и действие «◊» в изоморфном множестве В также дистрибутивно.

2. Понятие изоморфизма очевидным образом распространяется на алгебраические системы с несколькими действиями. Две универсальные алгебры (А, Ω) и (В, Ω¹), где А и В – множества, а Ω и Ω¹ – сигнатуры, изоморфны относительно своих сигнатур, если А и В изоморфны относительно каждой пары действий jⁱ и yⁱ из Ω и Ω¹ соответственно.

3. Если каждое из двух множеств с действиями изоморфны некоторому третьему множеству с действиями, то первые два изоморфны между собой относительно соответствующих действий.

Общая теория алгебраических действий распадается на ряд теорий, изучающих множества с тем или иным количеством действий, обладающих теми или иными свойствами (теория групп, полей, колец, алгебры Ли, булева алгебра, теория графов и т.д.).

§ 2.3. Свойства действий (операций)

Пусть в множестве А определено действие, обозначаемое «∘».

Действие называется неограниченно-применимым, если результат действия х ○ у определен для любой пары элементов х, у Î А, т.е. х ○ у Î А.

Действие называется коммутативным, если для любой пары элементов х, у Î А, для которых определен результат z = х ○ у Î А, обязательно определен и результат z ¢= у ○ х Î А, и при этом z = z ¢ (т.е. х ○ у = у ○ х).

Действие называется ассоциативным, если для любой тройки элементов х, у, z Î А, для которой определены результаты (х ○ у) и ((х ○ у)○ z), обязательно определены и результаты (у ○ z) и (х ○(у ○ z)), и наоборот. Причем выполняется равенство ((х ○ у)○ z)= (х ○(у ○ z)).

Действие называется обратимым, если для любой пары элементов х, у Î А всегда существуют такие u, v Î А, что определены результаты (х ○ u) и (v ○ х) и выполняются равенства (х ○ u)= y (обратимо справа) и (v ○ х)= y (обратимо слева).

Действие называется сократимым справа, если для любой тройки элементов х, у, z Î А, для которой определены результаты (х ○ z) и (у ○ z), равенство (х ○ z)=(у ○ z) выполняется тогда и только тогда, когда x = y. Аналогично, действие называется сократимым слева, если для любой тройки элементов х, у, z Î А, для которой определены результаты (z ○ x) и (z ○ y), равенство (z ○ x)=(z ○ y) выполняется тогда и только тогда, когда x = y. Если действие сократимо как справа, так и слева, то оно называется сократимым.

Элемент е _пÎ А называется нейтральным справа относительно данного действия, если для любого х Î А результат (x ○ е _п) определен и равен х. Аналогично, элемент е _лÎ А называется нейтральным слева относительно данного действия, если для любого х Î А результат (е _л○ x) определен и равен х. Элемент е Î А называется нейтральным относительно данного действия, если он является нейтральным как справа, так и слева одновременно, т.е. (е ○ x)=(x ○ е)= х для любого х Î А. При мультипликативной записи нейтральный элемент называется единицей и обозначается «1», при аддитивной записи – нулем и обозначается «0».

Элемент x ¢Î А называется обратным к элементу х Î А, если определены результаты (х ○ х ¢)и (х ¢○ х) и имеет место равенство (х ○ х ¢)= е (обратный справа) и (х ¢○ х)= е (обратный слева), где е – нейтральный элемент. Из этого определения следует, что (х ¢)¢= х. При мультипликативной записи обратный элемент обозначается «х ^-1», а при аддитивной – «– х».

Элемент x Î А называется идемпотентным, если результат (х ○ x) определен и равен х.

Заметим, что относительно данного действия в множестве может существовать лишь один нейтральный элемент. Действительно, если предположить, что е ₁ и е ₂ два нейтральных элемента, то для любого элемента х Î А, в том числе и для х = е ₂ Þ (е ₁○ е ₂)=(е ₂○ е ₁)= е ₂. И аналогично, для х = е ₁ Þ (е ₂○ е ₁)=(е ₁○ е ₂)= е ₁. Отсюда следует, что е ₁= е ₂ и, кроме того, обратным элементом к нейтральному является он сам.