Простейшие алгебраические системы

Алгебраические системы определяются множеством и заданными на нем действиями, обладающими теми или иными свойствами. Среди алгебраических систем некоторые выделяются в виду их особой важности и имеют особые наименования.

Множество, с заданным на нем бинарным действием называется группоидом или оперативом. Группоид называется частичным, если действие не обладает свойством неограниченной применимости; мультипликативным, если используется мультипликативная запись действия, и аддитивным в случае аддитивной записи действия.

Множество, в котором задано неограниченно – применимое и ассоциативное действие, называется полугруппой. Таким образом, полугруппа – это группоид с ассоциативным действием. При мультипликативной записи – с ассоциативным умножением, при аддитивной – с ассоциативным сложением.

Полугруппа с нейтральным элементом называется моноидом.

Множество, в котором задано неограниченно – применимое, ассоциативное и обратимое действие, называется группой. Таким образом, группа – это полугруппа с обратимым действием, т.е. для любых элементов x, y Î G найдутся элементы u, v Î G такие, что x ○ u = y и v ○ x = y. Группа (полугруппа) называется абелевой, если действие коммутативно. Для абелевых групп чаще используется аддитивная запись действия, т.е. " x, y, z Î G Þ (x + y)+ z = x +(y + z), x + y = y + x и " x, y Î G $ u, v Î G: x + u = y и v + x = y.

Теорема 2.4.1. (О группе)

1. В любой группе существует единица (нейтральный элемент) и при том только одна. Для любого элемента группы существует обратный элемент и при том только один.

2. Если в полугруппе существует нейтральный элемент и для любого её элемента существует обратный, то она является группой.

Доказательство:

1. Докажем сначала существование нейтрального элемента относительно действия в группе. Т.к. действие в группе обратимо, то для любых элементов x, y Î G найдутся элементы u, v Î G такие, что x ○ u = y и v ○ x = y. В том числе для у = х найдется е 'Î G и е '○ x = х, «домножим» обе части равенства x ○ u = y на е ' слева, тогда е '○(x ○ u)= е '○ у, но по ассоциативности е '○(x ○ u)=(е '○ x)○ u = x ○ u = у, т.о. у = е '○ у и е ' – левая единица. Аналогично, для у = х найдется е ''Î G и x ○ е ''= х. «Домножим» равенство v ○ x = y справа на е '', тогда (v ○ x)○ е ''= v ○(x ○ е '')= v ○ x = у, т.о. у = у ○ е '' и е '' – правая единица. Единственность нейтрального элемента была доказана ранее.

Теперь докажем существование и единственность обратного элемента для каждого элемента группы. В определении обратимости действия для любых элементов x, y Î G, а значит, в том числе и для у = е найдутся элементы u, v Î G такие, что x ○ u = е и v ○ x = е, т.е. u – обратный для х справа, а v – обратный слева. Покажем, что u = v. Действительно, умножим 1-ое на v слева, а 2-ое на u справа. Тогда v ○(x ○ u)= v ○ е и (v ○ x)○ u = e ○ u. По ассоциативности левые части обоих равенств одинаковы и, следовательно, v ○ е = e ○ u. Отсюда v = u, т.е. обратные элементы совпадают.

2. Пусть теперь G – полугруппа, е Î G – нейтральный элемент и для любого элемента х Î G существует обратный элемент х ¢Î G, т.е. х ○ х ¢= х ¢○ х = е. Рассмотрим произвольный элемент у Î G и элементы u = х ¢○ y и v = y ○ х ¢. Последние два равенства «умножим» на х слева и справа соответственно, тогда x ○ u = х ○(х ¢○ y) = (х ○ х ¢)○ y = е○ y = у и v ○ x = (y ○ х ¢)○ х = у ○(х ○ х ¢) = у ○ е = у. Тем самым, действие обратимо, как слева, так и справа, и G –группа.

Ввиду этой теоремы, можно дать эквивалентное определение группы:

Группа – это множество, в котором задано неограниченно – применимое и ассоциативное действие, существует нейтральный элемент относительно этого действия и для любого элемента имеется обратный.

Примеры алгебраических систем

1. Рассмотрим (ℕ,+). Так как сложение в множестве натуральных чисел неограниченно–применимо и ассоциативно, но нейтрального элемента по сложению не существует и ни у какого элемента нет обратного, то это полугруппа. Рассмотрим (ℤ,+), (ℚ,+), (ℝ,+), (ℂ,+). Все перечисленные множества образуют группу по сложению, т.к. имеется нейтральный элемент – это ноль и для всякого числа х имеется обратное число, равное (- х).

2. Рассмотрим (ℕ,´). Умножение во множестве натуральных чисел неограниченно–применимо и ассоциативно. Нейтральный элемент по умножению равен 1, обратный элемент имеется только у 1, поэтому это моноид.

(ℤ,´) – также моноид, (ℚ,´), (ℝ,´) – моноиды, здесь обратные имеют все элементы, кроме нуля, поэтому ℚ\{0} и ℝ\{0} образуют группы по умножению.

3. Рассмотрим 2 ^М – булеан произвольного множества М. Тогда (2 ^М,∪) – моноид. Так как объединение любых двух подмножеств М снова будет подмножеством М, т.е. объединение неограниченно–применимо. Для любых трех А, В, С Í М Þ (А ∪ В)∪ С = А ∪(В ∪ С), т.е. объединение ассоциативно, нейтральным элементом относительно объединения является Æ – пустое множество. Обратных элементов нет (кроме Æ). Аналогично (2 ^М,∩) – моноид, поскольку пересечение неограниченно–применимо на 2 ^М и ассоциативно. Нейтральным элементом относительно пересечения на 2 ^М является само множество М, но обратный элемент есть только для М.

4. Множество всех векторов на плоскости относительно операции сложения векторов образует группу, т.к. сложение векторов неограниченно–применимо, ассоциативно, нейтральным элементом является вектор нулевой длины, обратным элементом для каждого вектора по сложению является вектор той же длины, но противоположного направления.

5. Множество всех многочленов с коэффициентами, являющимися элементами произвольной группы, относительно операции сложения многочленов образует группу, т.к. для любых многочленов f (x) = a ₀ + a ₁ x + a ₂ x ²+…+ a_nxⁿ и g (x) = b ₀ + b ₁ x + b ₂ x ²+…+ b_nxⁿ их сумма (f (x)+ g (x)) = (a ₀+ b ₀) + (a ₁+ b ₁) x + (a ₂+ b ₂) x ²+…+(a_n + b_n) xⁿ – также многочлен. Сложение ассоциативно, нейтральный элемент – многочлен, все коэффициенты которого равны нулю, обратным к произвольному многочлену f (x) является многочлен [– f (x)], все коэффициенты которого имеют противоположные знаки.

6. Прямоугольные матрицы размера m ´ n, составленные из элементов произвольной группы, по отношению к операции сложения матриц образуют группу. Действительно, для любых матриц А и В размера m ´ n, результат сложения этих матриц также будет матрицей размера m ´ n. Ассоциативность сложения матриц следует из ассоциативности сложения их элементов. Нейтральным элементом по сложению является нулевая матрица (составленная из одних нулей). Обратная к произвольной матрице А_{m ´ n} составлена из тех же элементов, что и А_{m ´ n}, но с противоположными знаками.

7. Квадратные невырожденные (определитель которых не равен нулю) матрицы размера n ´ n с вещественными элементами образуют неабелеву (в отличие от всех предыдущих примеров) группу по отношению к операции умножения матриц. Здесь нейтральным элементом является так называемая единичная (по главной диагонали – единицы, в остальных местах – нули) матрица размера n ´ n. Для каждой матрицы А_{n ´ n} обратная может быть найдена по формуле 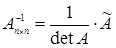, где det A – определитель матрицы А_{n ´ n} и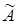– присоединенная матрица, определяемая следующим образом: 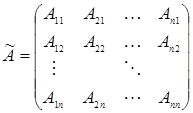, где А_ij – алгебраическое дополнение элемента a_ij матрицы А_{n ´ n}.

8. Группа преобразований – это множество всех биективных отображений произвольного множества Х на себя: F = { f: X ® X }, относительно операции композиции отображений. Действительно, если f и g – произвольные биекции Х на Х, то и результат композиции (f ∘ g) тоже биекция Х на Х. По свойствам композиции имеется ассоциативность, нейтральным элементом является тождественное отображение D={ (x, x): x Î X } такое, что для любого отображения f Î F имеет место равенство: f ∘ D = D∘ f = f. И для любого отображения f Î F существует обратное отображение f ^–1Î F, что f ∘ f ^–1= f ^–1∘ f = D. Эта группа не является коммутативной.

а) Пусть Х ={ 1, 2,¼, n }. Тогда биекции этого множества на себя – это различные перестановки элементов Х, так называемые подстановки. Композиция двух подстановок также является подстановкой, нейтральный элемент – тождественная подстановка 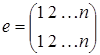и у каждой подстановки имеется обратная, например, для 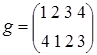обратная подстановка 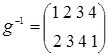и g ∘ g ^‑1= g ^–1∘ g = e. Группу подстановок называют также симметрической группой n ‑ой степени и обозначают обычно S_n. Эта группа не коммутативна.

б) Пусть Х – вещественная плоскость. Тогдамножество всех поворотов плоскости Х вокруг фиксированной точки образует абелеву группу относительно композиции поворотов. Действительно, ассоциативность поворотов следует из того, что соответствующие углы при этом складываются: (j+g)+d=j+(g+d). Нейтральным элементом является поворот на 0 градусов. Обратный поворот – это поворот на тот же угол, но в другом направлении. Если к поворотам добавить еще и отражение относительно всех прямых, проходящих через ту же фиксированную точку, то получится уже неабелева группа.