Основные теоремы теории вероятностей

Основные теоремы теории вероятностей позволяют по известным вероятностям простых событий определять вероятности более сложных событий.

Теорема 1. Теорема сложения вероятностей.

Вероятность суммы двух событий А и В равна сумме их вероятностей за вычетом вероятности произведения этих же событий

Р (А + В) = Р (А) + Р (В) – Р (А · В). (2.1)

Доказательство. Пусть исходы опыта образуют полную группу n несовместных равновозможных событий (рис.2.1). При этом

· m из них благоприятны событию А;

· k из них благоприятны событию В;

· l из них благоприятны произведению событий А · В.

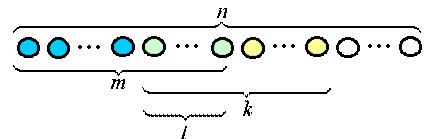
Рис.2.1

Тогда согласно классической формуле определения вероятности:

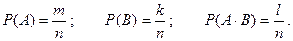
Согласно той же формуле вероятность появления события А или В

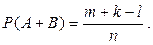
Преобразуем последнее равенство:

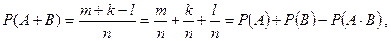
что и требовалось доказать.

Следствие теоремы 1. Вероятность суммы двух несовместных событий А и В равна сумме их вероятностей.

Следствие очевидно, поскольку произведение несовместных событий представляет собой невозможное событие, а вероятность невозможного события равна нулю:

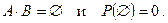
Следствие легко обобщается на случай нескольких событий.