Перевод чисел в десятичную систему: п ри переводе нужно пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо (начальный номер -1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда.
Пример.
а) Перевести 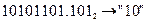 с.с.
с.с.
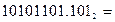
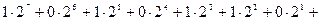
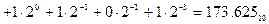
б) Перевести 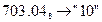 с.с.
с.с.
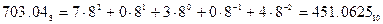
в) Перевести 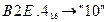 с.с.
с.с.
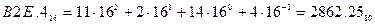 .
.
Перевод десятичных чисел в восьмеричную, шестнадцатеричную и двоичную системы Если переводится целая часть числа, то она делится на основание системы счисления, после чего запоминается остаток от деления. Полученное частное вновь делится на основание, остаток запоминается и т.д. до тех пор, пока частное не станет равным нулю. Остатки от деления записываются в порядке, обратном их получению.
Если переводится дробная часть числа, то она умножается на основание системы счисления, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на основание и т.д. до тех пор, пока дробная часть не станет равной нулю. Целые части записываются в порядке их получения.
Пример.
а) Перевести 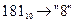 с.с.
с.с.
| 176 | |||
 5 5 | 16 | ||
| 0 | |||
Результат 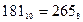 .
.
б) Перевести 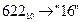 с.с.
с.с.
| 608 | |||
 14 14 | 32 | ||
| 0 | |||
Результат 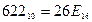 .
.
Пример.
Перевести 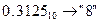 с.с.
с.с.
3125 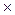 8 8 | |
5000 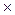 8 8 | |
 Результат
Результат 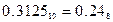 .
.
| 6 5´ 2 | |
| 3 ´ 2 | |
| 6 ´ 2 | |
| 2 ´ 2 | |
| 4 ´ 2 | |
| 8 ´ 2 | |
| 6 ´ 2 | |
| ... |
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести 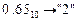 с.с. Точность 6 знаков.
с.с. Точность 6 знаков.
Результат 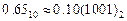 .
.
 Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример. Перевести 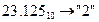 с.с.
с.с.
1) Переведем целую часть: 2) Переведем дробную часть:
 | |||||
| 0 | |||||
125 2 2 | |
25  2 2 | |
5  2 2 | |
 Таким образом
Таким образом 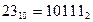 ;
; 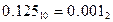 .
.
Результат: 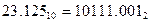 .
.
Необходимо отметить, что целые числа остаются целыми, а правильные дроби – дробями в любой системе счисления.
Пример.
а) 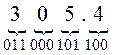
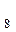 =
= 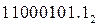 ;
;
Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.
б)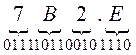
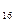 =
= 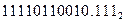 .
.
Для перехода от двоичной к восьмеричной или шестнадцатеричной системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример.
а) Перевести 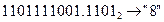 с.с.
с.с.
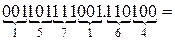
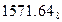
б) Перевести 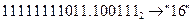 с.с.
с.с.
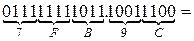
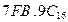
 2014-02-09
2014-02-09 1630
1630
