Суммарная погрешность механической обработки

ЛЕКЦИЯ № 11.

Литература

Лекция11. Суммарная погрешность механической обработки.

Лекция № 11. Суммарная погрешность механической обработки.

Тема № 5. ОСНОВЫ БАЗИРОВАНИЯ. ТОЧНОСТЬ ИЗГОТОВЛЕНИЯ ДЕТАЛЕЙ

Л Е К Ц И Я № 11

УТВЕРЖДАЮ

Заведующий кафедрой

«Технологии машиностроения»,

доцент _______________Чумак П.И.

«___» ____________________ 20__г.

Для студентов 4 курса

Специальности 151001 «Технология

машиностроения»

д.т.н., профессор Аверичкин Павел Алексеевич

(учёная степень, учёное звание, фамилия и инициалы автора)

(занятие № 16)

По дисциплине: «Основы технологии машиностроения»

	Лекция разработана: Профессором Аверичкиным П.А. _____________ Обсуждена на заседании кафедры: Протокол № ____ от «___» _________________ 20___г. Повторно с изменениями и дополнениями Рассмотрено: Протокол № ____ от «___» _________________ 20___г.

МГУПИ – 2009

Учебные и воспитательные цели:

1.Изложить сущность суммарных погрешностей.

2.Убедить, в важности выбора метода определения точности изготовления.

3. Ознакомить студентов с расчетами суммарной погрешности.

Время: 2 часа (90 мин.).

Место проведения Аудитория по расписанию.

Основная:

1. И.М.Колесов. Основы технологии машиностроения; Учебник для студентов высш. учеб. заведений М. Машиностроение, 1997,-592с.

2. Э.Л.Жуков, И.И.Козырь и др. Основы технологии машиностроения, В 2кн. Кн.1. Учебное пособие для вузов. М. ВШ. 2005. 278с.,ил.

3. Э.Л.Жуков, И.И.Козырь и др. Основы технологии машиностроения, В 2кн. Кн.2. Учебное пособие для вузов. М. ВШ. 2005. 295с.,ил.

Дополнительная:

4. В.В. Клепиков, А.Н. Бодров «Технология машиностроения» М. ФОРУМ -ИНФРА-М,2004

Учебно-материальное обеспечение:

1.Наглядные пособия: Плакат – Погрешности при изготовлении деталей. 2.Технические средства обучения: «Проектор».

3. Дополнительные материалы представлены в электроном виде и доступны для просмотра на компьютере.

ПЛАН ЛЕКЦИИ:

№ п/п	Вводная часть, рассматриваемые учебные вопросы, заключительная часть.	Время мин.
1. 2. 3.	Вводная часть. Значение точности в машиностроении. Повторение основных понятий и определений Задачи, решаемые при изготовлении деталей с учетом возникающих погрешностей. Основная часть. Суммарная погрешность механической обработки: решение задачи методом «максимума-минимума», векторным способом. Расчетно-статистический метод определения точности. Оценка различных методов. Расчет суммарной погрешности обработки. Заключительная часть. Подведение итогов работы Ответы на вопросы.

Лекция разработана «___»_____________20__г.

_______________________(Аверичкин П.А.)

(подпись, фамилия и инициалы автора)

1. Суммарная погрешность механической обработки: решение задачи методом «максимума-минимума», векторным способом.

2. Расчетно-статистический метод определения точности.

3. Оценка различных методов. Расчет суммарной погрешности обработки.

1.Суммарная погрешность механической обработки: решение задачи методом «максимума-минимума», векторным способом.

Суммарная погрешность при обработке на предварительно настро­енном станке.

Обрабатывается большая партия заготовок. Заготовки устанавливают в приспособление, и обработка ведется с большим числом настроек станка. Для этих условий суммарную погреш­ность или поле рассеяния выполняемого размера можно выразить в общем виде следующей функциональной зависимостью:

Δ = f (Δ_у, Δ_н, ε, Δ_и, Δ_т, Δ_ф).

Каждая из стоящих в скобках величин не зависит одна от дру­гой и для данного конкретного случая определяется условиями построения операции.

Погрешность Δ_у связана с упругими отжатиями технологичес­кой системы под влиянием нестабильности сил резания. При указанных пределах колебания припуска (глубины резания), твердости материала и сил резания в результате затуп­ления инструмента значение Δ_у можно рассчитать по вышеприве­денным зависимостям. Наибольшее значение Δ_у будет в тех сече­ниях заготовки, где жесткость технологической системы мини­мальна. Текущее значение Δ_у при обработке каждой заготовки (из партии однотипных заготовок) представляет собой величину случайную, распределение которой подчиняется нормальному за­кону.

Погрешность настройки станка Δ_н для данного метода обра­ботки регламентируется определенной величиной; зависит от метода настройки станка, квалификации наладчика и т.д. Величину Δ_н считают постоянной в пределах партии деталей, обработанных без поднастройки станка. В условиях массового про­изводства, когда имеют место многочисленные настройки и поднастройки станка, Δ_н является величиной случайной, распреде­ление которой подчиняется нормальному закону или закону, близ­кому к нему.

Погрешность установки заготовки ε складывается из погреш­ностей базирования, закрепления и положения заготовки в при­способлении. Для обработки индивидуальной заготовки погреш­ность ε будет выражена конкретным значением. Для партии заготовок будет иметь место рассеяние значений этой величины, обыч­но подчиняющееся закону нормального распределения. Одновре­менно для каждой индивидуальной заготовки в партии положе­ние измерительной базы будет случайным, в свя­зи с чем рассеяние значений ε в большинстве случаев подчиняет­ся нормальному закону.

Погрешности Δ_и, связанные с износом инструмента, относят к систематическим закономерно изменяющимся погрешностям. При обработке небольших и средних деталей рассеяние их разме­ров следует закону равной вероятности. Размеры деталей постоянно изменяются, достигая предельных значений, после чего нужно осуществлять подналадку станка или смену ин­струмента.

Погрешности Δ_т, связанные с тепловыми деформациями, наи­более полно проявляют себя в период разогрева технологической системы. Изменение (рассеяние) размеров деталей партии ориен­тировочно следует закону равной вероятности: имеет место систематическая закономерно изменяющаяся погреш­ность.

После наступления в системе теплового равновесия изменения размеров деталей замедляются или прекращаются вовсе, а вели­чина рассеяния Δ_т оказывается минимальной. В этот период по­грешность Δ_т рассматривают как величину систематическую, по­стоянную.

Перечисленные погрешности представляют собой пределы из­менения погрешностей, вызываемых теми или иными технологи­ческими факторами.

Величина Δ_ф есть сумма погрешностей формы данного эле­мента детали, вызываемая геометрическими неточностями стан­ка, деформациями заготовки при закреплении, неравномерными отжатиями технологической системы по пути резания (или в раз­ных сечениях заготовки). В процессе выполнения технологической операции над партией заготовок величина Δ_ф практически не из­меняется, т.е. одинакова для всех обработанных деталей.

Задача определения суммарной погрешности механической обработки подобна задаче нахождения допуска замыкающего раз­мера в размерном анализе. При решении ее методом максимума и минимума

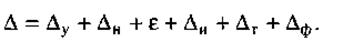
При одновременной параллельной обработке двух противоле­жащих элементов или при выполнении диаметральных размеров погрешность установки отсутствует (ε = 0). Величину Δ_ф определя­ют с учетом взаимной компенсации ее отдельных составляющих. Например, при консольном обтачивании валика из-за упругих отжатий возникает конусность его поверхности с вершиной со стороны передней бабки. Если направляющие станка не парал­лельны оси шпинделя, то при обработке образует­ся конусность с вершиной со стороны задней бабки станка. Обе погрешности компенсируют друг друга.

Расчет суммарной погрешности Δ методом максимума и мини­мума прост, но значения получаются завышенными. Даже при очень большом числе обрабатываемых заготовок предельные значения (наибольшие или наименьшие) суммы слагаемых погрешностей встречаются редко. Технологический допуск, принятый по вели­чине Δ(Т_Т > Δ), увеличивает промежуточные и общие припуски на обработку. По этой причине в технологии машиностроения при­нято рассматривать первые пять погрешностей как случайные ве­личины и суммировать их по законам математической статистики

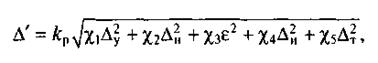
где k_p — коэффициент, определяющий процент риска Р_р полу­чения брака при обработке; при k_p = 1 вероятность возникнове­ния брака составляет

32 %, при k_p = 2 она снижается до 4,5 %, при k_p= 3 — до 0,27 % (рассеяние размеров в пределах ±3σ); χ₁…χ₅ — коэффициенты, зависящие от формы кривых распределения со­ответствующих элементарных погрешностей. Для кривых распре­деления по закону Гаусса (нормальное распределение)

χ = 1/9, по закону равной вероятности и в случае, когда о форме кривой рас­пределения ничего неизвестно, χ = 1/3, по закону Симпсона (форма треугольника) χ = 1/6.

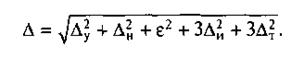Распределение величин Δ_у, Δ_н и ε близко к нормальному, тогда

χ₁ = χ₁ = χ₁= 1/9. Распределение Δ_н следует закону равной вероят­ности, а распределение Δ_т,. изучено недостаточно. Поэтому прини­мают χ₄ = χ₅ = 1/3. Приняв k_p = 3 (Р_р = 0,27 %), получают расчетную зависимость

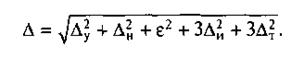С учетом погрешностей формы суммарная погрешность выполняемого размера

Если операцию обработки партии однотипных деталей выпол­няют на нескольких станках, то систематическая погрешность Δ_ф переходит в случайную и при определении суммарной погрешно­сти Δ квадрат Δ_ф вводится слагаемым под знак радикала.

При определении суммарной погрешности обработки диамет­р деталей без поднастройки станка (без смены и поднастройки инструмента) Δ_н → 0. При обработке малых партий мелких деталей погрешность Δ_и оказывается мень­ше заранее регламентированного (расчетного) значения; одно­временно уменьшается разность предельных значений припусков и твердости материала заготовок, для которых определяется вели­чина Δ_у.

Суммарная погрешность при обработке методом пробных ходов и промеров. При обработке заготовок указанным методом суммар­ная погрешность выполняемого размера

Δ = Δ_у + ε_инс + ε₃ + Δ_н + Δ_т + Δ_ст,

где Δу — погрешность формы обрабатываемой поверхности, полу­чаемая в результате копирования элементарных погрешностей за­готовки, в условиях упругой технологической системы, жесткость которой различна в различных сечениях; ε_инс — погрешность ус­тановки режущего инструмента на размер (погрешность провер­ки), зависящая от квалификации рабочего и вида применяемого измерительного инструмента; ε₃ — погрешность закрепления за­готовки или погрешность ее положения относительно измеритель­ной базы в результате деформации технологической системы от сил зажима; Δ_и — погрешность формы поверхности из-за размер­ного изнашивания режущего инструмента; Δ_т — погрешности фор­мы, вызываемые тепловыми деформациями технологической си­стемы в процессе обработки одной детали; Δ_ст — погрешность фор­мы обрабатываемой поверхности, возникающая из-за геометри­ческих неточностей станка.

В данном случае суммирование элементарных погрешностей вы­полняют алгебраически, учитывая возможность их частичного или полного перекрытия и взаимной компенсации.