2014-02-12
2543
2.4.1. Из трех мужчин (A, Б, В) и двух женщин (Г, Д) избирается комиссия из двух человек. Описать два различных пространства элементарных исходов этого эксперимента.
Решение.
а) Будем понимать под элементарным исходом список людей, которые вошливкомиссию. Тогда число элементарных исходов равно числу способов выбрать двух человек из пяти данных: т.е.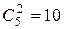 
. Выпишем явно множество W.
W = {(A, В), (A, Б), (A, Г), (A, Д), (Б, В), (Б, Г), (Б, Д), (B, Г), (B, Д), (Г, Д)}
Здесь записи (A, Б) или (Б, А) означают одно и то же.
б) Будем понимать под элементарным исходом число мужчин и число женщин, вошедших вкомиссию. Тогда возможны всего три случая: W =
= {(2М), (2Ж), (1М, 1Ж)}, где запись (1М, 1Ж), например, означает, чтовкомиссию вошли один мужчина и одна женщина.
2.4.2. Наугад выбирается одна буква из числа образующих слово «формула». Какие из следующих множеств являются пространством элементарных исходов для рассматриваемого эксперимента:
1) {ф, о, р, м, у, л, а}; 2) {р, м, у, л, а}; 3) (гласная, ф, р, м, л);
4) {согласная, у, е}; 5) (гласная, согласная)?
|
|
|
Решение. Если понимать под элементарным исходом выбранную букву, то первое множество можно считать пространством элементарных исходов,авторое нельзя, так как буквы «ф» и «о», которые могут быть выбраны,в данное множество не входят.
Пятое множество также можно считать пространством элементарных исходов, если понимать под элементарным исходом информацию о том, выбрана гласная или согласная буква.
Третье множество занимает промежуточное положение между первым и пятым. Под исходом эксперимента понимается информация о том, гласная или согласная буква выбрана, причем, если выбрана согласная буква, указывается, какая именно.
Четвертое множество не является пространством элементарных исходов для данного эксперимента.Внем не описаны возможности выбора букв «о» и «а», зато указана букса «е», которой нетв слове формула.
2.4.3. Поезда метро следуют с интерваломвдве минуты. Пассажир приходит на станциювслучайный момент времени.
Элементарный исход – время ожидания пассажиром поезда. Описать пространство элементарных исходов.
Решение. Элементарный исход – число из отрезка [0, 2], пространство элементарных исходов – множество точек отрезка [0, 2], W = { w | 0 £ w £
£ 2}.
2.4.5. А, В, С – три произвольных события. Найти выражения для событий, состоящихвтом, что из А, В, С:
1) произошло только А; 2) произошли A и В, событие С не произошло; 3) все три события произошли; 4) произошло по крайней мере одно из событий; 5) произошло одно и только одно событие; 6) ни одно из событий не произошло; 7) произошло не более двух событий; 8) произошло не менее двух событий.
Решение.
|
|
|
1. Произошел элементарный исход, благоприятствующий событию A и не благоприятствующий событиям B и С. Следовательно, произошло событие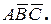 
2. Произошел элементарный исход, благоприятствующий событиям A и B и не благоприятствующий событию С. Следовательно, произошло событие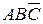 
.
3. Произошло событие ABC.
4. Произошел элементарный исход, благоприятствующий, по крайней мере, одному из событий: А, B или С, т.е. произошло событие (A + B + С).
5. Произошел элементарный исход, благоприятствующий ровно одному из трех событий, т.е. произошло событие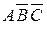 
+ 
+ 
.
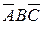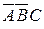6. Произошло событие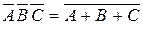 
.
7. Противоположное событие заключаетсявтом, что произошли все три события; значит, можно записать, что произошло событие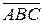 
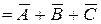. По-другому можно сказать так: хотя бы одно из событий не произошло.
8. Произошел элементарный исход, благоприятствующий по крайней мере двум из трех событий; значит, можно записать, что произошло событие (AВ + ВС + AC).
2.4.6. Событие A = {хотя бы одно из имеющихся четырех изделий бракованное}, событие B = {бракованных изделий среди них не менее двух}. Что означают события А \ В,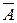 
, 
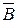? Можно ли сказать, что B Ì А?
Решение. Построим пространство элементарных исходов. Из условия задачи следует, что элементарным исходомвданном случае является количество бракованных изделий среди четырех данных. Тогда возможны 5 исходов. Обозначим их числами от 0 до 4; W = {0, 1, 2, 3, 4}; A = {1, 2, 3, 4}; B = {2, 3, 4}; А \ В = {1}; 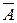= {0}; 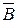= {0, 1}; А \ В = {среди четырех изделий ровно одно бракованное}; 
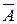= {все изделия годные}; 
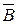= {среди четырех изделий менее двух бракованных}. Событие B Ì A.
