Теорема сложения вероятностей. Если события A и B совместны, AB ¹ Æ, вероятность суммы A + B определяется по формуле

Если события A и B совместны, AB ¹ Æ, вероятность суммы A + B определяется по формуле

p (A + В) = p (A) + p (B) – p (AB). (3.2)

Докажем эту формулу.

Пространство W состоит из n элементарных исходов, событие A содержит m_A элементарных исходов, событие B состоит из m_B элементарных исходов,апроизведению AB благоприятствуют m_AB исходов. Подсчитаем число исходов, благоприятствующих сумме A + В.

Событие A + B можно представитькак сумму трех несовместных собы-

тий: A + B = (A \ AB) + AB + (B \ AB) (рис. 3.1). В событие А \ АВ входят m_A –

- m_AB исходов; всобытие B \ AB входят m_B – m_AB исходов. Тогда p (A + В) =

= p (A \ АВ) + p (AB) + p (B \ АВ) = 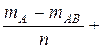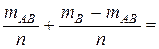p (A) +

+ p (B) – 2 p (AB) + p (AB) = p (A) + p (B) – p (AB), что и требовалось доказать.

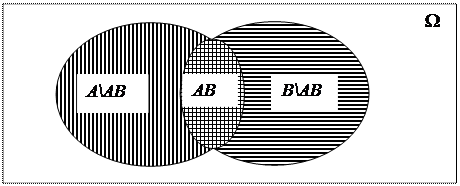Рис. 3.1