Теорема умножения вероятностей. Независимые события и условные вероятности

Независимые события и условные вероятности.

Пусть заданы пространство элементарных исходов W , содержащее n равновозможных элементарных исходов, событие А, содержащее m_A исходов, событие В, содержащее m_В исходов, и произведение AB, которому благоприятствуют m_AB исходов. Тогда

p(A) = m_A/n; p(B) = m_B/n; p(AB) = m_AB/n.

Известно, чтоврезультате эксперимента произошло событие А;вэтих условиях нужно найти новую вероятность события В. Такая вероятность обозначается символом p(B/А) и называется условной вероятностью события B при условии, что произошло событие А.

Если произошло событие А, то произошел один из m_A элементарных исходов, благоприятствующих этому событию. Следовательно, пространство элементарных исходов W сузилось до события A и содержит теперь не n,атолько m_A исходов. Bo множестве A событию B благоприятствуют исходы, входящиевпроизведение AB, их количество равно m_AB , поэтому

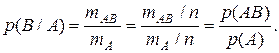(3.4)

В примере 3.4.1 определялась именно условная вероятность события В.

Формулу (3.4) можно записать по-другому:

p(AВ) = p(A) p(B/А) = p(B) p(A/В). (3.5)

Формула (3.5) выражает собой так называемую теорему умножения вероятностей.

События A и B называются независимыми тогда и только тогда, когда

p(A/В) = p(A), p(B/А) = p(B). (3.6)

В случае независимых событий A и B теорема умножения вероятностей записывается совсем просто:

p(AВ) = p(A) p(B). (3.7)

Рассмотрим такой пример. Эксперимент заключаетсявбросании двух игральных костей, W = {(1,1), (1, 2), ... , (6,6)} , n = 36. События A = {на первой кости выпало четное число очков} и B = {на второй кости выпало число очков, делящееся на 3} независимы, так как m_A = 18, m_B = 12, m_AB = 6, p(A) = 1/2, p(B) = 1/3, p(AВ) = 1/6, p(AВ) = p(A) p(B).

Этот результат соответствует интуитивным представлениям о независимости исхода бросания одной кости от исхода бросания другой.

События, которые не являются независимыми, называются зависимыми.