Модель с количественными скидками

Появляется возможность количественных скидок в зависимости от размера заказа. Рассматривается зависимость издержек хранения от цены товара. Оптимальный уровень заказа определяется исходя из условия минимизации общих издержек для каждого вида скидок.

Модели типа 1-5 с вероятностным распределением
спроса и времени выполнения заказа

Вместо предпосылки о постоянстве и детерминированности спроса на товар используется более реалистичный подход о предполагаемой известности распределения темпа спроса и времени выполнения заказа.

Рассмотрим подробнее модели с фиксированным размером заказа.

Модель 1. Наиболее экономичного размера заказа. Заказ, пополняющий запасы, поступает как одна партия. Уровень запасов убывает с постоянной интенсивностью пока не достигает нуля. В этой точке поступает заказ, размер которого равен Q, и уровень запасов восстанавливается до максимального значения. При этом оптимальным решением задачи будет тот размер заказа, при котором минимизируются общие издержки за период (рис.6.1).

Пусть Q - размер заказа; Т - протяженность периода планирования; D - величина спроса за период планирования; d - величина спроса в единицу времени; К - издержки заказа; Н - удельные издержки хранения за период; h - удельные издержки хранения в единицу времени. Тогда:

(D/Q)K - совокупные издержки заказа;

(Q/2)H - совокупные издержки хранения;

d = D/T; h = H/T;

Q* =(2dK/h)^1/2 (2DK/H)^1/2 - оптимальный размер заказа;

N = D/Q* - оптимальное число заказов за период;

t* = Q*/d = T/N - время цикла (оптимальное время между заказами).

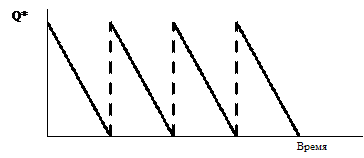Рис. 6.1. Модель 1. Наиболее экономичного размера заказа

Модель 2. Введем предположение о том, что заказ может быть получен не мгновенно, а с течением времени. Тогда нам необходимо заранее делать заказ, чтобы в нужное время иметь достаточное количество товара на складе. Следовательно, нам необходимо найти тот уровень запасов, при котором делается новый заказ. Этот уровень называется точкой восстановления R. Пусть L - время выполнения заказа. Тогда R = величина спроса в единицу времени, умноженная на время выполнения заказа = d L. Другие характеристики системы определяются так же, как и в модели 1. Модель иллюстрируется рис.6.2.

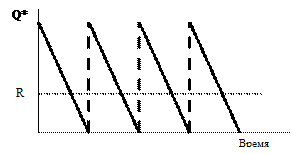Рис. 6.2. Модель 2