2014-02-12
769
Рис. 6.4. Модель 4
Рис.6.3. Модель 3
Пусть р - упущенная прибыль в единицу времени, возникающая в результате дефицита одной единицы продукта; Р - упущенная прибыль за период, возникающая в результате дефицита одной единицы продукта.
Тогда:Q* = (2dK/h)1/2 x ((р+h)/р)1/2=(2DK/H)1/2 х ((Р+Н)/P)1/2 - оптимальный размер заказа; S* = (2dK/h)1/2 x (р/(h+р))1/2 =(2DK/H)1/2 x (P/(H+P))1/2 - максимальный размер запаса;R = Q*- S* - максимальный дефицит.
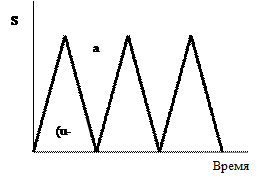Модель.4 производства и распределения. В предыдущей модели мы допускали, что пополнение запаса происходит единовременно. Но в некоторых случаях, особенно в промышленном производстве, для комплектования партии товаров требуется значительное время и производство товаров для пополнения запасов происходит одновременно с удовлетворением спроса. Такой случай показан на рис.6.4.
Спрос и производство являются частью цикла восстановления запасов. Пусть u - уровень производства в единицу времени, К - фиксированные издержки производства.
Тогда:
совокупные издержки хранения = (средний уровень запасов) х Н = Q/2[1-d/u] Н;
средний уровень запасов = (максимальный уровень запасов)/2;
максимальный уровень запасов = u t - d t = Q(l - d/u);
время выполнения заказа t = Q/u;
издержки заказа = (D/Q) К;
оптимальный размер заказа Q* = (2dK/h [(l-(d/u)])1/2 = (2DK/H[(l-(d/u)])1/2;
максимальный уровень запасов S* = Q*[(l-(d/u)].
Модель 5. Модель с количественными скидками. Для увеличения объема продаж компании часто предлагают количественные скидки своим покупателям.
Количественная скидка - сокращенная цена на товар в случае покупки большого количества этого товара. Типичные примеры количественных скидок приведены в табл.8.1.
Таблица 6.1
| Варианты скидок | |||
| Количество, при котором делается скидка | от 0 до 999 | от 1000 до 1999 | от 2000 и выше |
| Размер скидки, % | |||
| Цена со скидкой | 4,8 | 4,75 |
Пусть I - доля издержек хранения в цене продукта с.
Тогда h = (I x c) и Q* = (2dK/(I x c))1/2 - оптимальный размер заказа.
Рассмотрим пример, объясняющий принцип принятия решения в условиях скидки. Магазин "Медвежонок" продает игрушечные гоночные машинки. Эта фирма имеет таблицу скидок на машинки в случае покупок их в определенном количестве (табл. 6.1). Издержки заказа составляют 49 тыс. р. Годовой спрос на машинки равен 5000. Годовые издержки хранения в отношении к цене составляют 20%, или 0,2. Необходимо найти размер заказа, минимизирующий общие издержки.
