Правило моментов для токов

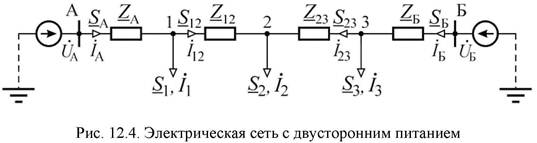
Рассмотрим небольшую электрическую сеть с двусторонним питанием (рис. 12.4). Нагрузки узлов 1, 2, 3 заданы комплексными значениями расчетных токов. Напряжения узлов А и Б одинаковые ().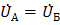

Предположим, что под воздействием нагрузок в узлах токи в ветвях приняли указанные на схеме направления. В соответствии со вторым законов Кирхгофа можно записать

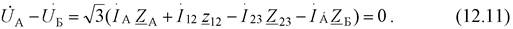По балансовым соотношениям первого закона Кирхгофа выразим токи в ветвях (на участках) сети через известные токи нагрузок в узлах и искомый ток на головном участке сети :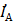

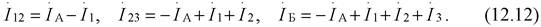Подставив токи из выражения (12.12) в (12.11):

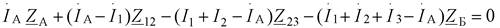и выполнив математическое преобразование, получим

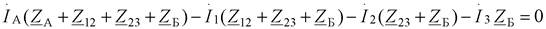Обозначим:

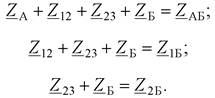Тогда: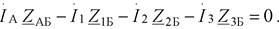

Отсюда ток головного участка А:

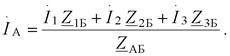Или в общем виде для сети, содержащей n нагрузочных узлов, можно записать

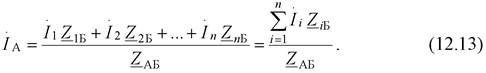Правило моментов может быть аналогично применено и для определения тока на головном участке Б. В этом случае моменты токов находят относительно узла А:

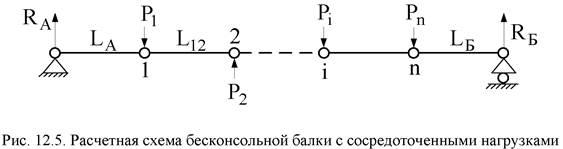
Выражения (12.13), (12.14) получили название правила моментов для токов. Действительно, для вычисления, например, тока источника А рассчитывают моменты токов по отношению к противоположному источнику Б. Эти выражения аналогичны выражению для определения реакции (ответа) R_А, R_Б опор бесконсольной балки:

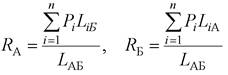при воздействии на нее сосредоточенных механических нагрузок (сил) P_i (рис. 12.5).

В формулах (12.13), (12.14) токи в узлах выступают в роли механических нагрузок, а сопротивления ветвей от точки подключения нагрузки до узла Б или (А) – в роли плеча.

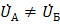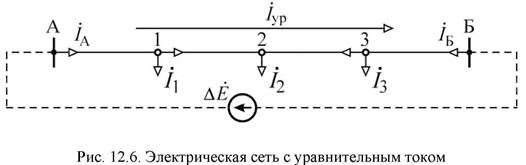
Рассмотрим случай неравенства напряжений () источников. Под воздействием ЭДС, равной разнице напряжений 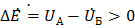, в схеме протекает уравнительный ток (рис. 12.6)

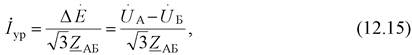с учетом которого скорректируем токи источника (головных участков):

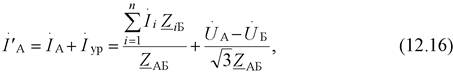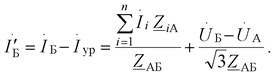Таким образом, результирующий ток источника образуется двумя слагаемыми: первое слагаемое обусловлено нагрузками в узлах и соотношениями сопротивлений отдельных участков сети, второе слагаемое тока определяется разностью напряжений источников, сопротивлением всей сети и не зависит от величины и места подключения нагрузок.