Определение. Подмножество  кольца
кольца  называется подкольцом кольца
называется подкольцом кольца  и обозначается
и обозначается 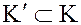 , если
, если  является кольцом относительно операций сложения и умножения, определенных в кольце
является кольцом относительно операций сложения и умножения, определенных в кольце  .
.
В каждом кольце 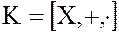 , очевидно, существуют следующие подкольца:
, очевидно, существуют следующие подкольца:
· само кольцо  ;
;
· нулевое кольцо 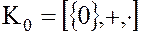 , где
, где 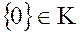 .
.
Для выяснения, является ли данное подмножество  кольца
кольца  подкольцом этого кольца, можно воспользоваться следующей теоремой.
подкольцом этого кольца, можно воспользоваться следующей теоремой.
Теорема. Для того, чтобы непустое подмножество  кольца
кольца 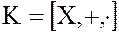 было его подкольцом, необходимо и достаточно выполнение следующих двух условий:
было его подкольцом, необходимо и достаточно выполнение следующих двух условий:
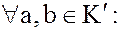
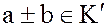 (10)
(10)
( – подгруппа аддитивной группы кольца
– подгруппа аддитивной группы кольца  );
);
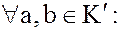
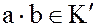 (11)
(11)
( – подполугруппа мультипликативной полугруппы кольца
– подполугруппа мультипликативной полугруппы кольца  ).
).
Доказательство. Докажем необходимость условий.
Предположим, что  - подкольцо кольца
- подкольцо кольца  .
.
Пусть 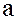 и
и 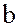 – произвольные элементы подмножества
– произвольные элементы подмножества  .
.
Тогда каждый из элементов
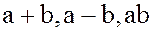
кольца  содержится в
содержится в  :
:
если бы по крайней мере один из них не содержался бы в  , то подмножество
, то подмножество  не было бы кольцом относительно операций, определенных на
не было бы кольцом относительно операций, определенных на  , и, следовательно, не было бы подкольцом кольца
, и, следовательно, не было бы подкольцом кольца  .
.
|
|
|
Докажем достаточность условий. Предположим, что подмножество  удовлетворяет условиям теоремы.
удовлетворяет условиям теоремы.
Тогда в подмножестве  определено понятие суммы и произведения, т.е. на подмножестве
определено понятие суммы и произведения, т.е. на подмножестве  определены операции сложения и умножения.
определены операции сложения и умножения.
Эти операции на подмножестве  ассоциативны, коммутативны и связаны дистрибутивным законом:
ассоциативны, коммутативны и связаны дистрибутивным законом:
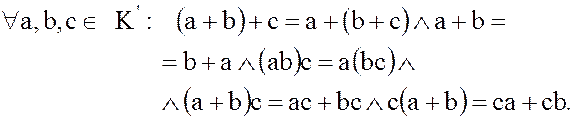
Нулевой элемент 0 содержится в  и для
и для 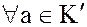 обратный (противоположный) элемент
обратный (противоположный) элемент 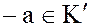 .
.
Действительно, пусть 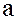 – произвольный элемент подмножества
– произвольный элемент подмножества  .
.
Тогда 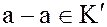 т.е.
т.е. 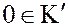 и
и 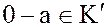 , т.е.
, т.е. 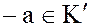 .
.
Таким образом, подмножество  является кольцом относительно операций сложения и умножения, определенных на
является кольцом относительно операций сложения и умножения, определенных на  и, следовательно, является подкольцом кольца
и, следовательно, является подкольцом кольца  .
.
Примеры. 1. Кольцо четных целых чисел 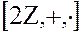 является подкольцом кольца целых чисел –
является подкольцом кольца целых чисел – 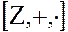 .
.
2. Кольцо целых чисел 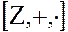 является подкольцом кольца рациональных чисел –
является подкольцом кольца рациональных чисел – 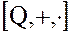 .
.
3. Кольцо рациональных чисел 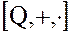 и кольцо
и кольцо 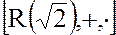 , где, как и ранее,
, где, как и ранее, 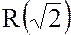 – множество чисел вида
– множество чисел вида 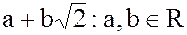 , являются подкольцами кольца действительных чисел –
, являются подкольцами кольца действительных чисел – 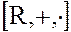 .
.
Для любого семейства подколец произвольного кольца справедливо следующее утверждение.
Теорема. Пересечение любого семейства подколец 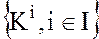 кольца
кольца  является подкольцом кольца
является подкольцом кольца  :
:
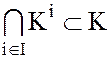 . (12)
. (12)
Доказательство. Нулевой элемент 0 кольца  содержится в каждом из подколец, и, следовательно, содержится в их пересечении.
содержится в каждом из подколец, и, следовательно, содержится в их пересечении.
Если  – кольцо с единицей, то каждое подкольцо
– кольцо с единицей, то каждое подкольцо 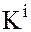 кольца
кольца  также будет содержать единицу кольца, и, следовательно, и их пересечение будет содержать единицу кольца.
также будет содержать единицу кольца, и, следовательно, и их пересечение будет содержать единицу кольца.
Пусть 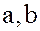 – произвольные элементы, принадлежащие
– произвольные элементы, принадлежащие 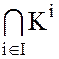 . Элементы
. Элементы 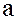 и
и 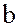 , очевидно, содержатся в каждом из подколец
, очевидно, содержатся в каждом из подколец 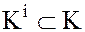 .
.
По определению кольца, элементы 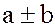 и
и 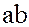 также содержатся в каждом из подколец
также содержатся в каждом из подколец 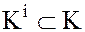 , следовательно
, следовательно 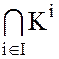 – удовлетворяет аксиомам кольца и является подкольцом кольца
– удовлетворяет аксиомам кольца и является подкольцом кольца  .
.
|
|
|
Пусть, как и ранее, произвольное множество 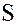 содержится в каждом из подколец
содержится в каждом из подколец 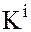 кольца
кольца  :
:
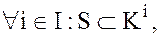
тогда можно определить минимальное подкольцо 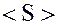 , содержащее заданное множество
, содержащее заданное множество 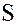 :
:
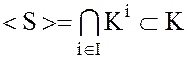 (13)
(13)
Если 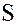 – подкольцо кольца, то
– подкольцо кольца, то 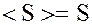 .
.
 2014-02-13
2014-02-13 4873
4873







