Кольцо целостности

Кольцо классов вычетов

Важнейшие типы колец

Пусть 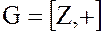– аддитивная группа целых чисел, а 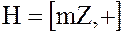– подгруппа целых чисел, делящихся на 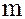без остатка.

Ранее мы показали, что разбиение группы 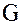по подгруппе 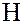определяет фактормножество

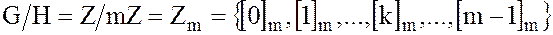, (14)

элементы которого 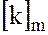являются классы вычетов по модулю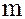

т.е. левые смежные классы аддитивной группы целых чисел 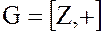по подгруппе

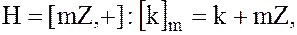
где .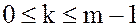

На множестве 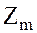– классов вычетов по модулю 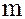определены операции сложения 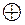и умножения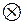

по модулю :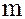

(15)

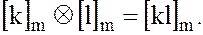(16)

Так как выполнение этих операций сводится к соответствующим операциям над числами из классов вычетов, т.е. над элементами из 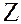_m,

то 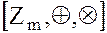будет коммутативным кольцом с единицей .

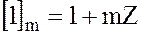Определение. Кольцо 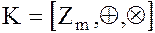называется кольцом классов вычетов по модулю m.

Вводя обозначения 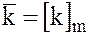при фиксированном m, операции сложения и умножения можно записать в сокращённой форме:

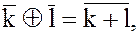(17)

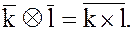(18)

При записи операций сложения и умножения на классе вычетов по модулю 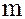можно отказаться и от чёрточек и кружочков и оперировать с каким-либо фиксированным множеством представителей классов вычетов по модулю m.

Чаще всего в качестве такого множества представителей выступает множество 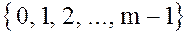, – которое называется приведенной системой вычетов по модулю m.

Пусть 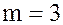, тогда таблицы Кэли для операций сложения и умножения в кольце 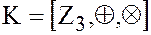имеют вид:

					.

Кольцо 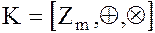классов вычетов по модулю 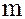играет в алгебре важную роль и служит отправным пунктом для многочисленных обобщений.

Пусть – произвольное кольцо с единицей .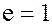

Как было показано ранее, для любого элемента 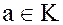выполняются равенства:

.

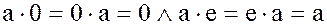Отсюда следует, что нулевой – 0 и единичный – 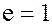элементы являются различными элементами кольца.

Если для элемента 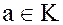в кольце существует обратный элемент , то он единственный, для которого выполняется условие

.

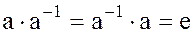Единичный элемент 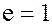кольца является обратным для самого себя:

.

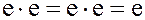Из равенства

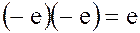
следует, что элемент 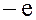также является обратным для самого себя.

Нулевой элемент 0 кольца не имеет обратного элемента, поскольку

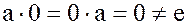, для любого элемента .

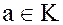Определение. Элемент 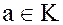, для которого в кольце существует, и притом только единственный, обратный элемент , называют обратимым или делителем единицы.

Кольцо целых чисел является самым простым примером коммутативного кольца, в котором только 1 и –1 являются делителями единицы .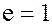

Теорема. Множество всех делителей единицы 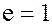кольца является группой по умножению.

Доказательство. Действительно, если 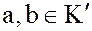, т.е. являются делителями единицы кольца , то

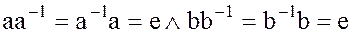
и, следовательно,

.

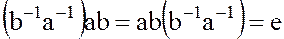А это означает, что 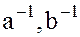и 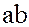также являются делителями единицы и, следовательно, содержатся в множестве . Поэтому множество является группой по умножению.

Определение. Группа называется группой делителей единичного элемента 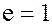кольца .

Так как для любого элемента 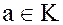выполняется равенство

,

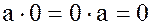то по определению делителей элементов кольца, каждый элемент является делителем нуля.

В теории колец для произвольных элементов 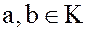используют следующее определение делителей нуля.

Определение. Элементы 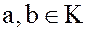называются делителями нуля, если 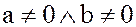, а 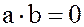; при этом 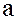называют левым, а 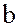– правым делителем нуля.

Пример. 1. В кольце 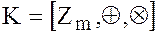классов вычетов по mod m существуют делители нуля:

в кольце классов вычетов по mod 6 :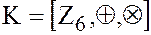

,

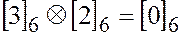в кольце классов вычетов по mod 4 :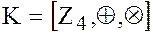

.

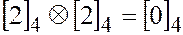2. В кольце квадратных матриц второго порядка также существуют делители нуля:

пусть ,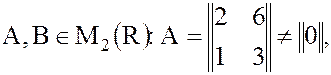

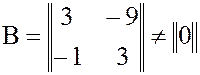тогда .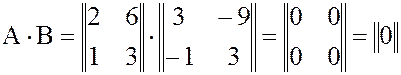

Определение. Кольцом (областью) целостности называется коммутативное кольцо без делителей нуля.

Пример. 1. 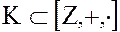– кольцо целых чисел является кольцом целостности.

2. Кольцо 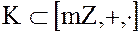является кольцом целостности в том и только в том случае, если 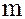– простое число.

Рассмотрим произвольное кольцо .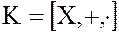

Есл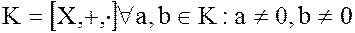и , и 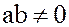, т.е. кольцо не содержит делителей нуля, то такое кольцо называется телом.

Более строго.

Определение. Кольцо K, в котором для всех отличных от нуля элементов существуют обратные, называется телом.

Тело не содержит делителей нуля, т.е. есл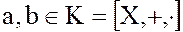и и – тело, то, если .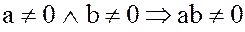

Это означает, что отличные от нуля элементы тела образуют полугруппу по умножению.

Более того, т.к. тело содержит единичный элемент и для каждого отличного от нуля элемента в теле существует обратный элемент, то элементы тела, отличные от нуля образуют группу по умножению.

Примеры. 1. Тело рациональных чисел 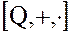. Действительно, если

,

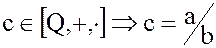где .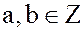

Если .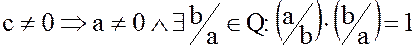

Важно, чтобы обратный элемент .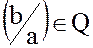

Для любого целого числа, например 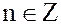, обратный элемент существует и равен 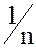, но он не принадлежит .

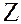2. Тело вещественных чисел.

3. Тело комплексных чисел.

Кольцом целостности, с которым наиболее часто приходится встречаться, является кольцо целых чисел .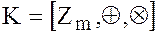

В теории колец особую роль играют кольца, которые по своим свойствам достаточно близки к кольцу целых чисел.