Деление многочленов

Кольцо многочленов 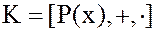с вещественными коэффициентами близко к кольцу целых чисел .

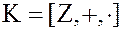Эта аналогия проявляется в том, что для многочленов, как и для целых чисел, имеются понятия деления нацело, деление с остатком, делителя, наибольшего общего делителя (НОД) и др.

Теорема. Для любых двух многочленов 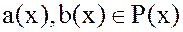, где 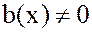, существует, и притом единственная, пара многочленов 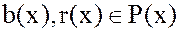, такая, что 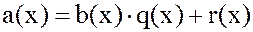, где либо 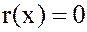, либо .

Эта теорема очень похожа на теорему о делимости целых чисел. По аналогии с целыми числами многочлен 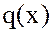называется частным (если 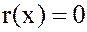) или неполным частным (если 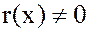). А 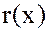- остатком от этого деления.

Если 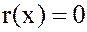, то говорят, что 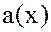нацело делится 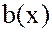, при этом 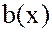называется делителем 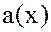. Очевидно, что делителями любого многочлена 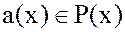будут:

1. Все многочлены нулевой степени, т.е. 1.

2. Все многочлены вида 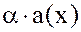, где .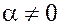

Определение. Многочлен 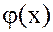называется общим делителем многочленов 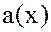и 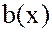, если он является делителем каждого из них.

Замечание. Очевидно, все многочлены нулевой степени – общие делители для любой пары многочленов.