Пусть K – некоторое коммутативное кольцо.
Определение. Стандартным многочленом (или полиномом) степени 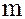 от одной переменной x над коммутативным кольцом K называется выражение вида
от одной переменной x над коммутативным кольцом K называется выражение вида
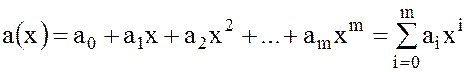 , (23)
, (23)
где 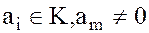 .
.
Элементы 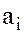 называются коэффициентами многочлена. Все они, или часть из них, могут быть нулевыми.
называются коэффициентами многочлена. Все они, или часть из них, могут быть нулевыми.
Каноническая форма многочлена (23) определяется следующим образом.
Находим наибольшее 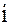 , такое, что
, такое, что 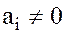 , скажем
, скажем 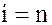 и запишем
и запишем
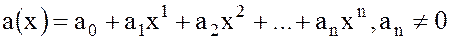 (24)
(24)
Степенью многочлена 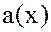 называется число
называется число 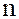 , если оно существует.
, если оно существует.
Если же все 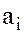 обращаются в нуль, то канонической формой многочлена является 0.Число
обращаются в нуль, то канонической формой многочлена является 0.Число 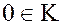 по определению считается многочленом с нулевыми коэффициентами и называется нулевым многочленом. Степень нулевого многочлена неопределенна.
по определению считается многочленом с нулевыми коэффициентами и называется нулевым многочленом. Степень нулевого многочлена неопределенна.
Степень многочлена 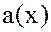 обозначается
обозначается 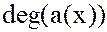 (дигри).
(дигри).
В зависимости от того, какому из множеств принадлежат коэффициенты 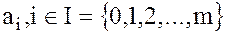 , различаются следующие типы многочленов:
, различаются следующие типы многочленов:
· с булевыми коэффициентами 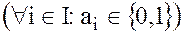 ;
;
· с целочисленными коэффициентами 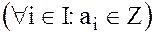 ;
;
· с вещественными коэффициентами 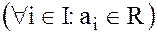 ;
;
· с рациональными коэффициентами 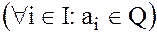 ;
;
· с комплексными коэффициентами 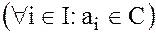 .
.
Пусть 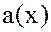 и
и 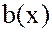 - два многочлена:
- два многочлена:
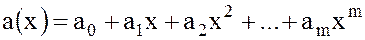
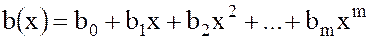
Определение. Многочлены 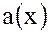 и
и 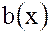 равны тогда и только тогда, когда
равны тогда и только тогда, когда 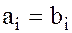
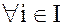 , при которых
, при которых 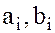 определены, а все остальные
определены, а все остальные 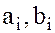 , равны нулю.
, равны нулю.
Обозначение 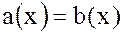 .
.
Из определения равенства многочленов 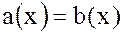 следует:
следует:
1.Нулевой многочлен равен только нулевому многочлену.
2.Для ненулевых многочленов
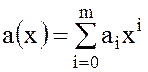
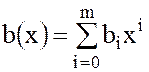
равенство 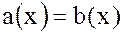 означает, что
означает, что
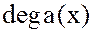 =
=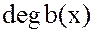 =m и
=m и 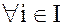 :
: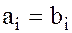 .
.
Замечание. Равенство многочленов определённое таким образом означает тождественное или формальное равенство в отличие от равенства многочленов как функций.
Множество всех многочленов от переменной x с вещественными переменными обозначим 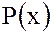 .
.
Тогда
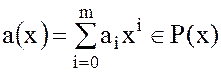 ,
,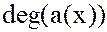 =m.
=m.
На множестве всех многочленов от переменной x с вещественными переменными 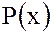 определены две алгебраические операции –сложение и умножение многочленов.
определены две алгебраические операции –сложение и умножение многочленов.
Пусть имеется два многочлена 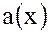 степени
степени 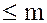 и
и 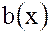 степени
степени 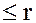 .
.
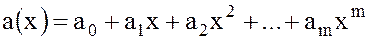
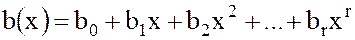
Определение. Суммой двух многочленов 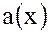 и
и 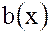 называется многочлен
называется многочлен
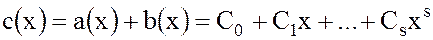 (25)
(25)
где 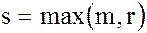 и
и
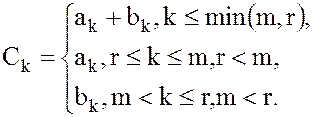 (26)
(26)
Из определения суммы многочленов следует:
1.Для любого многочлена
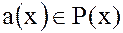 :
: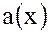 +0=0+
+0=0+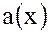 ;
;
2. Для ненулевых многочленов 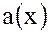 и
и 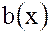
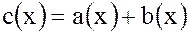 :
: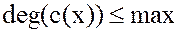 (
(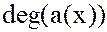 ,
,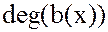 );
);
3.Если
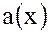 ,
, 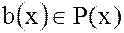 ,то
,то 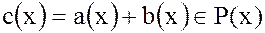
т. е. операция сложения многочленов 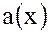 и
и 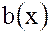 является алгебраической операцией на множестве всех многочленов
является алгебраической операцией на множестве всех многочленов 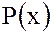 .
.
Определение. Произведением двух многочленов 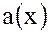 и
и 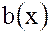 называется многочлен
называется многочлен
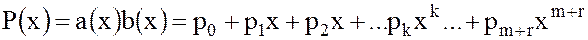 , (27)
, (27)
где 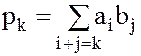 .
.
Замечание. Суммированиев
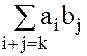
ведётся по всем индексам i и j, для которых i+j=k.
Из определения умножения многочленов следует:
1. Произведение ненулевых многочленов не может быть нулевым, при этом
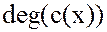 =
=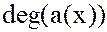 +
+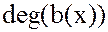
2. Если 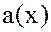 ,
, 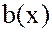
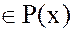 , то
, то 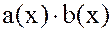
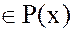 , т.е. умножение многочленов является алгебраической операцией на множестве
, т.е. умножение многочленов является алгебраической операцией на множестве 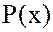 .
.
3. Операция умножения многочленов с вещественными коэффициентами порождает операцию умножения многочлена на число из 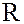 как частный случай умножения многочленов. Если
как частный случай умножения многочленов. Если 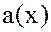
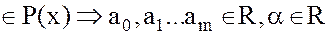 , то
, то
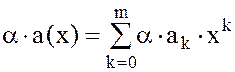
Теорема. Множество 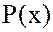 всех многочленов с коэффициентами из
всех многочленов с коэффициентами из 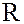 является коммутативным кольцом с единицей и без делителей нуля.
является коммутативным кольцом с единицей и без делителей нуля.
Доказательство. Проверим все аксиомы кольца.
1. 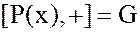 - аддитивная абелева группа. Коммутативность и ассоциативность сложения очевидны (2). Нулем является нулевой многочлен. Противоположным (обратным) к многочлену
- аддитивная абелева группа. Коммутативность и ассоциативность сложения очевидны (2). Нулем является нулевой многочлен. Противоположным (обратным) к многочлену 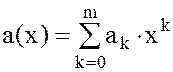 является многочлен
является многочлен 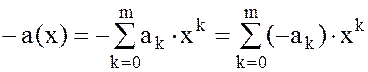 .
.
2. 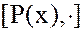 - моноид (полугруппа с единицей).
- моноид (полугруппа с единицей).
2.1. Коммутативность умножения следует из определения.
2.2. Докажем ассоциативность умножения.
Пусть 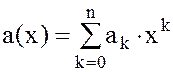 ,
, 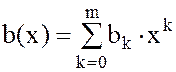 ,
, 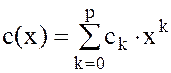
Рассмотрим произведение многочленов
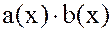 =
= 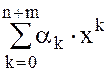 , где
, где 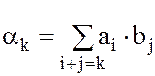
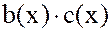 =
= 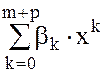 , где
, где 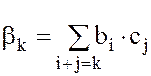
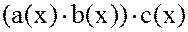 =
=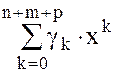 ,
,
где 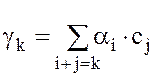 =
= 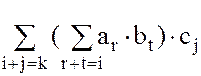 =
= 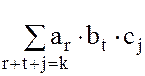
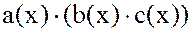 =
= 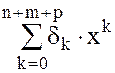 , где
, где 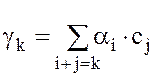 =
=
= 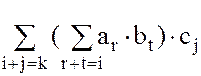 =
= 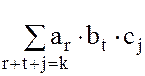
Учитывая, что
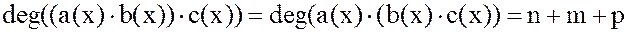 ,
,
операция умножения многочленов из 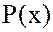 - ассоциативна.
- ассоциативна.
2.3 Роль единицы при умножении многочленов играет число
1, рассматриваемое как многочлен нулевой степени.
2.4 Справедливость аксиом дистрибутивности вытекает из
равенства
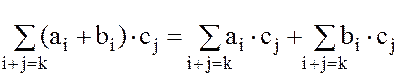 , (3)
, (3)
так как левая часть равенства (3) является коэффициентом при 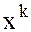 в многочлене
в многочлене
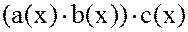 ,
,
а правая часть - коэффициентом при 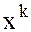 в многочлене
в многочлене
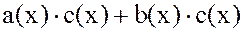 .
.
Замечание. Произведение многочленов 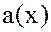 и
и 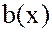 может быть получено обычным для элементарной алгебры перемножением двух сумм
может быть получено обычным для элементарной алгебры перемножением двух сумм
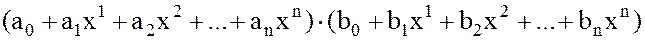
с последующей группировкой одночленов одинаковых степеней.
 2014-02-13
2014-02-13 2308
2308








