Выясним какие идеалы есть в простейшем кольце – кольце целых чисел  . Любое целое число
. Любое целое число 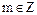 порождает главный идеал
порождает главный идеал 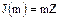 . Такими идеалами исчерпывается множество всех идеалов кольца
. Такими идеалами исчерпывается множество всех идеалов кольца 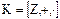 , поскольку справедлива следующая теорема.
, поскольку справедлива следующая теорема.
Теорема. Каждый идеал кольца целых чисел является главным идеалом.
Доказательство. Пусть 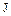 – некоторый идеал кольца
– некоторый идеал кольца 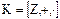 – целых чисел. Если
– целых чисел. Если 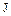 – нулевой идеал, то
– нулевой идеал, то 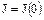 . Если же в идеале
. Если же в идеале 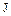 содержится число
содержится число 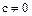 , то в нем содержится также и число
, то в нем содержится также и число 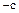 . Одно из чисел
. Одно из чисел 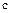 или
или 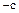 положительное, поэтому в идеале
положительное, поэтому в идеале 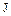 содержатся натуральные числа. Пусть
содержатся натуральные числа. Пусть  – наименьшее из натуральных чисел, содержащихся в
– наименьшее из натуральных чисел, содержащихся в 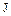 . Тогда
. Тогда
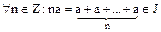 (3.72)
(3.72)
и, следовательно, 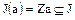 .
.
Докажем и обратное включение. Действительно, пусть 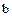 – произвольный элемент из идеала
– произвольный элемент из идеала 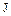 кольца
кольца 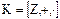 . Разделив
. Разделив 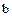 на
на  , получим
, получим 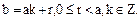 Поскольку
Поскольку 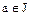 и
и 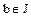 , то
, то 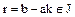 . Отсюда и из условия
. Отсюда и из условия 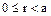 следует, что
следует, что 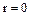 , так как в противном случае
, так как в противном случае  не было бы наименьшим среди натуральных чисел, содержащихся в идеале
не было бы наименьшим среди натуральных чисел, содержащихся в идеале 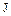 . Таким образом,
. Таким образом, 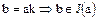 и, следовательно,
и, следовательно, 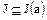 . Таким образом
. Таким образом
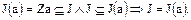
Пусть 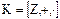 – кольцо целых чисел, а
– кольцо целых чисел, а 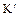 – произвольное кольцо с единицей
– произвольное кольцо с единицей 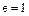 . Рассмотрим отображение
. Рассмотрим отображение
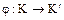 (3.73)
(3.73)
вида 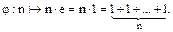
Очевидно, что отображение 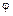 является гомоморфизмом кольца целых чисел
является гомоморфизмом кольца целых чисел  в кольцо
в кольцо 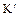 .
.
Множество 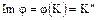 является подкольцом кольца
является подкольцом кольца 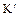 и состоит из всех целых кратных
и состоит из всех целых кратных 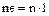 единичного элемента
единичного элемента 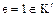 . Это подкольцо
. Это подкольцо 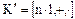 будем называть подкольцом, порожденным единичным элементом
будем называть подкольцом, порожденным единичным элементом 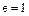 кольца
кольца 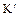 . В этом случае отображение
. В этом случае отображение 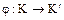 является гомоморфизмом кольца целых чисел
является гомоморфизмом кольца целых чисел 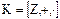 на подкольцо
на подкольцо 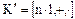 кольца
кольца 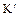 .
.
Поэтому по теореме о гомоморфизме колец, подкольцо 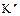 изоморфно фактор-кольцу
изоморфно фактор-кольцу 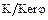 , где
, где 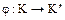 . Поскольку в кольце целых чисел
. Поскольку в кольце целых чисел 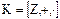 каждый идеал
каждый идеал 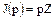 главный, то
главный, то 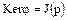 , где
, где  – некоторое неотрицательное число. Возможны два случая:
– некоторое неотрицательное число. Возможны два случая:
· 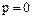 . Тогда
. Тогда 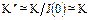 т.е. подкольцо
т.е. подкольцо 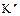 изоморфно кольцу целых чисел;
изоморфно кольцу целых чисел;
· 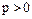 . Тогда
. Тогда 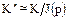 т.е. подкольцо
т.е. подкольцо 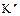 изоморфно кольцу классов вычетов по модулю
изоморфно кольцу классов вычетов по модулю  .
.
Следовательно, в любом кольце  с единицей
с единицей 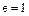 подкольцо
подкольцо 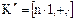 порожденное элементом
порожденное элементом 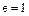 , изоморфно или кольцу целых чисел
, изоморфно или кольцу целых чисел 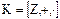 или кольцу классов вычетов по модулю
или кольцу классов вычетов по модулю  :
: 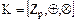 , где
, где  – некоторое натуральное число. Пусть
– некоторое натуральное число. Пусть  – некоторое кольцо с единицей
– некоторое кольцо с единицей 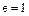 .
.
Определение. Характеристикой кольца 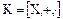 называется порядок подгруппы, порожденной единицей в аддитивной группе
называется порядок подгруппы, порожденной единицей в аддитивной группе 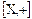 кольца
кольца  .
.
Замечание. В случае, если группа порожденная единицей кольца, бесконечна, принято говорить, что кольцо имеет характеристику нуль, а не бесконечность. Числовые кольца 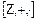 ,
, 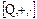 ,
, 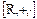 ,
, 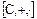 имеют характеристику нуль, а кольцо классов вычетов по модулю
имеют характеристику нуль, а кольцо классов вычетов по модулю  :
: 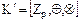 имеет характеристику
имеет характеристику  .
.
Определение. Кольцо  имеет характеристику 0, если его подкольцо
имеет характеристику 0, если его подкольцо 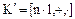 порожденное единичным элементом
порожденное единичным элементом 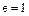 , изоморфно кольцу целых чисел
, изоморфно кольцу целых чисел 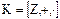 .
.
Определение. Кольцо  имеет характеристику
имеет характеристику  если его подкольцо
если его подкольцо 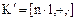 изоморфно кольцу классов вычетов по модулю
изоморфно кольцу классов вычетов по модулю 
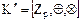 .
.
По определению, кольцо целых чисел 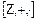 имеет характеристику 0, а кольцо
имеет характеристику 0, а кольцо 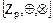 – классов вычетов по модулю
– классов вычетов по модулю  имеет характеристику
имеет характеристику  .
.
Замечание. Наряду с высказыванием «кольцо  имеет характеристику 0 (или
имеет характеристику 0 (или  )» применяют также высказывания «характеристика кольца
)» применяют также высказывания «характеристика кольца  равна 0 (или р)», «
равна 0 (или р)», « является кольцом характеристики 0 (или р)»
является кольцом характеристики 0 (или р)»
Теорема. Если кольцо  имеет характеристику 0, то
имеет характеристику 0, то 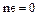 только при
только при 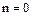 ; если же
; если же  имеет характеристику
имеет характеристику  , то
, то 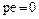 и нет такого натурального числа
и нет такого натурального числа 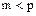 , что
, что 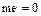 .
.
Доказательство. Пусть  — кольцо характеристики 0 Тогда существует изоморфное отображение
— кольцо характеристики 0 Тогда существует изоморфное отображение 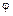 подкольца
подкольца 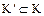
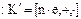 на кольцо
на кольцо 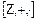 – целых чисел. Поскольку по теореме 6 при гомоморфизме
– целых чисел. Поскольку по теореме 6 при гомоморфизме 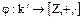 (в частности, изоморфизме) кольца
(в частности, изоморфизме) кольца 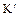 на кольцо
на кольцо 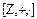 , то
, то 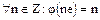 . Поэтому
. Поэтому 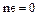 только при
только при 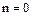 , ибо если
, ибо если 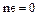 , то
, то 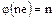 , по теореме 6, равно 0, т. е.
, по теореме 6, равно 0, т. е. 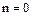 .
.
Предположим, что  — кольцо характеристики р. Тогда существует изоморфное отображение
— кольцо характеристики р. Тогда существует изоморфное отображение  кольца
кольца 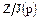 на подкольцо
на подкольцо 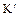 . По теореме 6,
. По теореме 6, 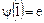 , где
, где 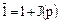 , и поэтому
, и поэтому 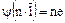 . Поскольку
. Поскольку 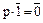 и по теореме 6
и по теореме 6 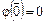 , то
, то 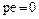 . Если
. Если 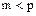 , то
, то 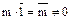 , а поэтому и
, а поэтому и 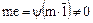 , так как в противном случае отображение
, так как в противном случае отображение  было бы гомоморфизмом, а не изоморфизмом.
было бы гомоморфизмом, а не изоморфизмом.
Справедлива также и обратная теорема.
Теорема. Если в кольце  с единицей
с единицей 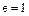 равенство
равенство 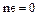 справедливо только при
справедливо только при 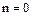 , то
, то  имеет характеристику 0; если в кольце
имеет характеристику 0; если в кольце  справедливо равенство
справедливо равенство 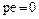 и нет такого натурального
и нет такого натурального 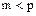 , что
, что 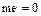 , то
, то  имеет характеристику р.
имеет характеристику р.
Доказательство. Рассмотрим гомоморфизм 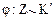 , для которого
, для которого 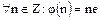 . По теореме о гомоморфизмах колец
. По теореме о гомоморфизмах колец 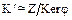 , где
, где 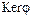 — ядро гомоморфизма
— ядро гомоморфизма 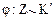 . Если в
. Если в  равенство
равенство 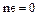 справедливо только при
справедливо только при 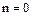 , то при гомоморфизме
, то при гомоморфизме 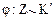 в нуль кольца
в нуль кольца 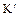 отображается только 0 кольца
отображается только 0 кольца 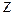 ; поэтому
; поэтому 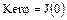 и, следовательно,
и, следовательно, 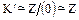 , т. е.
, т. е. 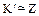 . Если в кольце
. Если в кольце  справедливо равенство
справедливо равенство 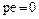 и нет такого натурального
и нет такого натурального 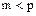 , что
, что 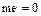 , то при гомоморфизме
, то при гомоморфизме 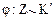 в ноль кольца
в ноль кольца 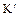 отображаются все целые кратные
отображаются все целые кратные 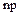 числа
числа  и только они; поэтому
и только они; поэтому 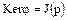 и
и 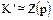 .
.
Из теорем 9 и 10 вытекает следующее определение.
Определение. Характеристикой кольца  с единицей
с единицей 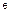 называют число 0, если
называют число 0, если 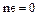 только при
только при 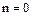 ; характеристикой кольца
; характеристикой кольца  называют натуральное число
называют натуральное число  , если
, если 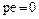 и нет такого натурального числа
и нет такого натурального числа 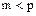 , что
, что 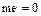 .
.
Все числовые кольца с единицей, очевидно, имеют характеристику 0. Каждое конечное кольцо  с единицей
с единицей 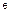 является кольцом ненулевой характеристики. Действительно, если кольцо
является кольцом ненулевой характеристики. Действительно, если кольцо  конечно, то среди всех целых положительных кратных единичного элемента
конечно, то среди всех целых положительных кратных единичного элемента 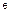 обязательно будут кратные, равные между собой, так как в противном случае кольцо
обязательно будут кратные, равные между собой, так как в противном случае кольцо  было бы бесконечным. Пусть.
было бы бесконечным. Пусть. 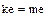 , где
, где 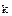 и
и 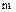 – некоторые натуральные числа, причем
– некоторые натуральные числа, причем 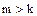 . Тогда
. Тогда 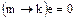 и, следовательно,
и, следовательно,  является кольцом ненулевой характеристики.
является кольцом ненулевой характеристики.
Каждое натуральное число 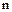 является характеристикой некоторого кольца с единицей:
является характеристикой некоторого кольца с единицей: 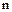 является характеристикой кольца
является характеристикой кольца 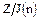 . Докажем теперь две теоремы, которые характеризуют свойства колец характеристики 0 и характеристики
. Докажем теперь две теоремы, которые характеризуют свойства колец характеристики 0 и характеристики  .
.
Теорема. Если 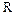 является областью целостности характеристики 0, то
является областью целостности характеристики 0, то
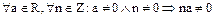 .
.
Доказательство. Пусть  – произвольно выбранный, отличный от 0, элемент из
– произвольно выбранный, отличный от 0, элемент из 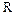 и
и 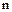 – любое натуральное число. Тогда
– любое натуральное число. Тогда
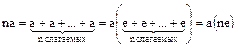 .
.
Предположим, что 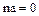 , тогда и
, тогда и 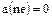 . Поскольку в
. Поскольку в 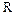 нет делителей нуля и по условию теоремы
нет делителей нуля и по условию теоремы 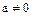 , то из равенства
, то из равенства 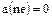 вытекает, что
вытекает, что 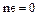 , чего не может быть. Следовательно,. предположение, что
, чего не может быть. Следовательно,. предположение, что 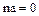 , неправильное. Таким образом, для любого натурального
, неправильное. Таким образом, для любого натурального 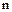 имеем
имеем 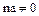 . При любом целом отрицательном
. При любом целом отрицательном 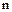 также
также 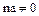 , ибо если бы элемент
, ибо если бы элемент 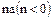 кольца
кольца 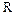 был равен нулю, то и противоположный ему элемент
был равен нулю, то и противоположный ему элемент 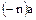 также был бы равен нулю, чего по доказанному выше не может быть.
также был бы равен нулю, чего по доказанному выше не может быть.
Теорема. Если 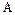 – кольцо характеристики
– кольцо характеристики  , то
, то
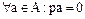 .
.
Доказательство. Действительно,
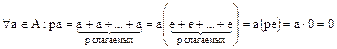 .
.
Эти кольца получили название колец главных идеалов. Пусть 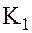 – кольцо целостности с единицей – коммутативное кольцо без делителей нуля, в котором понятие правого и левого делителя элемента совпадают. Определение делимости элементов этого кольца можно сформулировать так:
– кольцо целостности с единицей – коммутативное кольцо без делителей нуля, в котором понятие правого и левого делителя элемента совпадают. Определение делимости элементов этого кольца можно сформулировать так:
Определение. Если для элементов 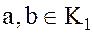 кольца целостности
кольца целостности 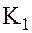 в кольце
в кольце 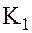 существует такой элемент
существует такой элемент 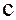 , что
, что 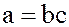 , то говорят, что элемент
, то говорят, что элемент 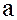 делится на
делится на 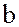 , и пишут
, и пишут 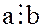 или
или 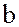 делит
делит 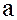 , и пишут
, и пишут 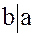 , или
, или 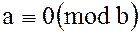 .
.
Из определения делимости двух элементов вытекают следующие свойства делимости в кольце целостности :
:
1. 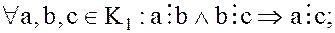
2. 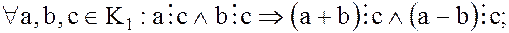
3. 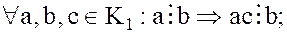
4. 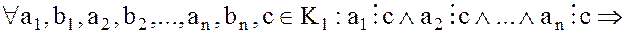
Эти свойства являются распространением на кольцо целостности 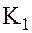 соответствующих свойств делимости в кольце целых чисел.
соответствующих свойств делимости в кольце целых чисел.
5. Каждый элемент 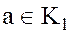 делится на любой делитель
делится на любой делитель  единицы
единицы 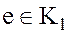 . Действительно, если
. Действительно, если 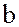 – делитель единицы, то и
– делитель единицы, то и 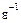 – также делитель единицы, а это означает, что
– также делитель единицы, а это означает, что 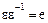 , тогда
, тогда 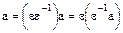 и, следовательно,
и, следовательно, 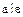 .
.
6. Если 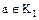 делится на
делится на  , то
, то  делится и на
делится и на 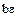 , где
, где 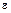 – любой делитель единицы.
– любой делитель единицы.
Действительно, из равенства 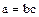 следует равенство
следует равенство 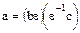 и, следовательно,
и, следовательно, 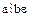 .
.
7. Каждый элемент из делителей  и
и 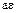 , где
, где 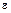 – любой делитель единицы, является делителем и другого.
– любой делитель единицы, является делителем и другого.
Действительно, из равенства 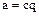 следует равенство
следует равенство 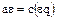 , а из равенства
, а из равенства 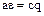 – равенство
– равенство 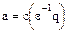 . Следовательно, если
. Следовательно, если 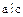 , то
, то 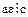 , и наоборот.
, и наоборот.
В дальнейшем будем рассматривать элементы кольца целостности  , отличные от нуля.
, отличные от нуля.
Определение. Элементы 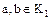 кольца целостности
кольца целостности  называются ассоциированными, если каждый из них является делителем другого:
называются ассоциированными, если каждый из них является делителем другого:
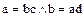 . (55)
. (55)
Из равенства (55) следует, что 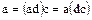 . Отсюда, сократив обе части полученного равенства на
. Отсюда, сократив обе части полученного равенства на 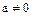 , получаем
, получаем 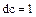 . Следовательно,
. Следовательно, 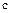 и
и 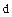 являются делителями единицы. Таким образом, если
являются делителями единицы. Таким образом, если  и
и 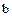 – ассоциированные элементы, то
– ассоциированные элементы, то 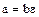 , где
, где 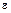 – некоторый делитель единицы. С другой стороны, какой бы мы не взяли делитель единицы
– некоторый делитель единицы. С другой стороны, какой бы мы не взяли делитель единицы 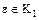 , элементы
, элементы  и
и 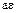 ассоциированные между собой, поскольку
ассоциированные между собой, поскольку 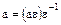 .
.
Определение. Элементы 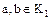 кольца целостности
кольца целостности  называются ассоциированными, если
называются ассоциированными, если 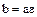 , где
, где 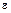 – некоторый делитель единицы.
– некоторый делитель единицы.
Пример. В кольце целых чисел 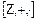 ассоциированными являются пары чисел
ассоциированными являются пары чисел 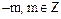 .
.
Если  и
и 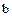 ассоциированные элементы кольца целостности
ассоциированные элементы кольца целостности , то
, то 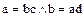 . Отсюда следует, что
. Отсюда следует, что 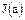 – главный идеал, порожденный элементом
– главный идеал, порожденный элементом  является подмножеством
является подмножеством 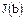 – главного идеала, порожденного элементом
– главного идеала, порожденного элементом 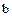 и наоборот:
и наоборот:
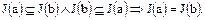
Это означает, что два ассоциированных элемента 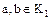 , кольца целостности
, кольца целостности  порождают один и тот же главный идеал.
порождают один и тот же главный идеал.
Пусть 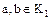 – произвольные элементы кольца целостности
– произвольные элементы кольца целостности  .
.
Определение. Элемент 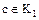 называется общим делителем элементов
называется общим делителем элементов  и
и 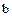 , если каждый из этих элементов делится на
, если каждый из этих элементов делится на 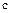 .
.
По свойству 5 все делители единицы 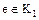 кольца целостности
кольца целостности  являются общими делителями элементов
являются общими делителями элементов  и
и 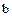 . Но у элементов
. Но у элементов  и
и 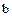 могут быть и другие общие делители. Введем понятие наибольшего общего делителя (НОД) этих элементов. Определение НОД двух целых чисел, по которому НОД называют наибольший из общих делителей, распространить на кольцо целостности нельзя, т.к. в произвольном кольце целостности
могут быть и другие общие делители. Введем понятие наибольшего общего делителя (НОД) этих элементов. Определение НОД двух целых чисел, по которому НОД называют наибольший из общих делителей, распространить на кольцо целостности нельзя, т.к. в произвольном кольце целостности 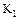 нет отношения порядка. Однако можно ввести и другое определение НОД двух чисел
нет отношения порядка. Однако можно ввести и другое определение НОД двух чисел  и
и 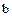 , а именно: НОД двух чисел
, а именно: НОД двух чисел  и
и 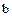 называется такой общий делитель этих чисел, который делится на любой другой их общий делитель. Именно это определение НОД и распространяется на элементы кольца целостности
называется такой общий делитель этих чисел, который делится на любой другой их общий делитель. Именно это определение НОД и распространяется на элементы кольца целостности  .
.
Определение. Наибольшим общим делителем двух элементов 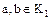 кольца целостности
кольца целостности  называется такой элемент
называется такой элемент 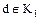 , обозначаемый символом
, обозначаемый символом 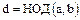 и обладающий двумя свойствами:
и обладающий двумя свойствами:
1. 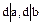 ;
;
2. 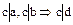 .
.
Замечание. Ясно, что вместе с 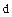 свойствами 1., 2. Обладает любой ассоциированный с ним элемент. Действительно, если
свойствами 1., 2. Обладает любой ассоциированный с ним элемент. Действительно, если 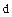 – НОД элементов
– НОД элементов 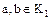 , то формально это записывается в виде
, то формально это записывается в виде 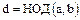 или
или 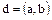 . Если также и
. Если также и 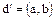 , то элементы
, то элементы 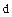 и
и 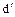 делятся друг на друга и, следовательно, являются ассоциированными. С другой стороны, если
делятся друг на друга и, следовательно, являются ассоциированными. С другой стороны, если 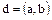 , то, очевидно,
, то, очевидно, 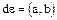 , где
, где 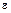 – любой делитель единицы. Таким образом НОД элементов
– любой делитель единицы. Таким образом НОД элементов 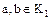 определяется с точностью до сомножителя
определяется с точностью до сомножителя 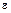 , который является делителем единицы.
, который является делителем единицы.
С учетом этого замечания к свойствам 1., 2. Наибольшего общего делителя добавляются следующие:
3. 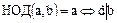 ;
;
4. 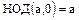 ;
;
5. 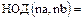
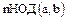 ;
;
6. 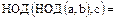
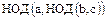 .
.
Свойство 6. позволяет распространить понятие НОД на произвольное конечное число элементов кольца целостности  .
.
По аналогии с 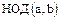 вводится дуальное понятие наименьшего общего кратного
вводится дуальное понятие наименьшего общего кратного 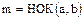 элементов
элементов 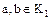 кольца целостности
кольца целостности  определенного с точностью до ассоциированности и обладающее также двумя свойствами:
определенного с точностью до ассоциированности и обладающее также двумя свойствами:
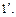
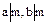 ;
;
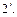
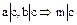 .
.
В частности, полагая 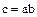 , получаем, что
, получаем, что 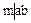 .
.
Теорема. Если для элементов 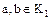 кольца целостности
кольца целостности  существуют
существуют 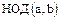 и
и 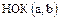 . Тогда
. Тогда
а) 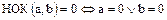 ;
;
б) 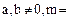
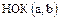 ,
, 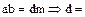
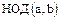 .
.
Доказательство. Утверждение а) вытекает непосредственно из определения 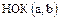 . Для доказательства б) необходимо убедиться, что элемент
. Для доказательства б) необходимо убедиться, что элемент 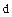 , определенный равенством
, определенный равенством 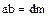 , обладает свойствами 1., 2. НОД. Действительно, из
, обладает свойствами 1., 2. НОД. Действительно, из 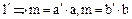 , следовательно
, следовательно 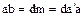 , откуда после сокращения на
, откуда после сокращения на  , допустимого в любом кольце целостности
, допустимого в любом кольце целостности  , имеем
, имеем 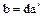 , т.е.
, т.е. 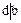 . Аналогично
. Аналогично 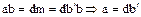 , т.е.
, т.е. 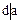 . Этим доказано свойство 1. Для доказательства свойства 2. Представим
. Этим доказано свойство 1. Для доказательства свойства 2. Представим 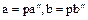 . Положим
. Положим 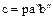 . Тогда
. Тогда  – общее кратное элементов
– общее кратное элементов  и
и 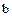 . Согласно свойству
. Согласно свойству 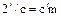 для некоторого
для некоторого 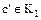 , откуда
, откуда 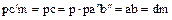 , т.е.
, т.е. 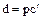 и
и 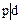 , что и требовалось доказать.
, что и требовалось доказать.
Определение. Элементы 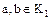 кольца целостности
кольца целостности  называются взаимно простыми, если они не имеют общих делителей, отличных от делителей единицы, т.е. если НОД
называются взаимно простыми, если они не имеют общих делителей, отличных от делителей единицы, т.е. если НОД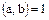 .
.
Пусть 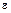 – произвольный делитель единицы, и
– произвольный делитель единицы, и 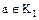 – произвольный элемент кольца целостности
– произвольный элемент кольца целостности  . Тогда из условия
. Тогда из условия 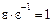 следует, что
следует, что 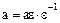 . Это означает, что все элементы ассоциированные с элементом
. Это означает, что все элементы ассоциированные с элементом  , и все делители единицы являются делителями элемента
, и все делители единицы являются делителями элемента 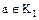 . Их называют тривиальными или несобственными делителями элемента
. Их называют тривиальными или несобственными делителями элемента  . Все делители отличные от
. Все делители отличные от 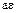 и
и 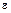 , если такие существуют в
, если такие существуют в  , называются нетривиальными, или собственными делителями элемента
, называются нетривиальными, или собственными делителями элемента 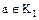 .
.
Пример. В кольце целых чисел 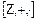 тривиальными делителями числа 10 являются числа
тривиальными делителями числа 10 являются числа 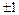 и
и 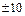 , а нетривиальными – числа
, а нетривиальными – числа 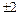 и
и 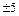 .
.
Определение. Элемент 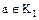 кольца целостности
кольца целостности  называется неразложимым, или простым, если он не является делителем единицы и не имеет нетривиальных делителей; элемент
называется неразложимым, или простым, если он не является делителем единицы и не имеет нетривиальных делителей; элемент 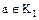 называется разложимым, или составным, если он имеет нетривиальные делители.
называется разложимым, или составным, если он имеет нетривиальные делители.
Другими словами, элемент 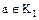 называется разложимым, если его можно представить в виде произведения
называется разложимым, если его можно представить в виде произведения 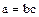 двух нетривиальных делителей
двух нетривиальных делителей 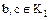 ; элемент
; элемент 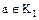 – называется неразложимым, если его нельзя представить в виде произведения двух нетривиальных делителей.
– называется неразложимым, если его нельзя представить в виде произведения двух нетривиальных делителей.
Пример. В кольце целых чисел 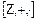 неразложимыми являются числа
неразложимыми являются числа 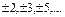 т.е. простые числа и противоположные простым. Все остальные числа отличные от
т.е. простые числа и противоположные простым. Все остальные числа отличные от 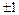 , – разложимы.
, – разложимы.
Неразложимые элементы обладают следующими свойствами:
· если элемент 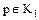 кольца целостности
кольца целостности  неразложимый, то и любой ассоциированный с ним элемент
неразложимый, то и любой ассоциированный с ним элемент 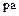 также неразложимый;
также неразложимый;
· если 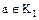 – произвольный элемент кольца целостности
– произвольный элемент кольца целостности  , а
, а 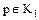 – неразложимый элемент из
– неразложимый элемент из  , то или
, то или  делится на
делится на  , или
, или  и
и  – взаимно простые элементы из
– взаимно простые элементы из  .
.
Действительно, первое свойство следует непосредственно из свойства 7 делимости элементов кольца целостности. Второе свойство докажем следующим образом. Если НОД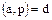 , то
, то 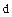 как делитель неразложимого элемента
как делитель неразложимого элемента  , является либо некоторым делителем единицы
, является либо некоторым делителем единицы 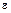 , либо элементом вида
, либо элементом вида 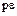 . В первом случае элементы
. В первом случае элементы  и
и  взаимно простые, во втором –
взаимно простые, во втором –  делится на
делится на  .
.
Определение. Кольцо целостности  называется кольцом с однозначным разложением на простые множители (или факториальным кольцом), если любой элемент
называется кольцом с однозначным разложением на простые множители (или факториальным кольцом), если любой элемент 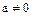 из
из  можно представить в виде:
можно представить в виде:
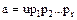 , (46)
, (46)
где 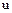 обратный элемент, а
обратный элемент, а 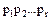 – простые элементы (не обязательно попарно различные), причем из существования другого такого разложения
– простые элементы (не обязательно попарно различные), причем из существования другого такого разложения
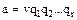
следует, что 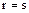 и при надлежащей нумерации элементов
и при надлежащей нумерации элементов 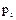 и
и 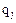 будет
будет
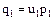 ,
,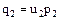 ,…,
,…,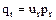 ,
,
где 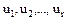 – обратные элементы в
– обратные элементы в  . Допуская в разложении (46)
. Допуская в разложении (46) 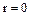 , мы принимаем соглашение, что обратимые элементы
, мы принимаем соглашение, что обратимые элементы 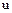 в кольце целостности
в кольце целостности  также имеют разложение на простые множители. Ясно, что если
также имеют разложение на простые множители. Ясно, что если  – простой, а
– простой, а 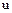 обратный элемент в
обратный элемент в  , то ассоциированный с
, то ассоциированный с  элемент
элемент 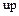 тоже простой.
тоже простой.
Пример. В кольце целых чисел 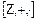 с обратимыми элементами
с обратимыми элементами 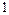 и
и 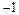 отношение порядка
отношение порядка 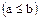 дает возможность выделить положительное простое число
дает возможность выделить положительное простое число  из двух возможных простых элементов
из двух возможных простых элементов 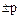 .
.
Теорема. Пусть  – произвольное кольцо целостности с разложением на простые множители. Однозначность разложения в
– произвольное кольцо целостности с разложением на простые множители. Однозначность разложения в  (факториальность
(факториальность  ) имеет место тогда и только тогда, когда любой простой элемент
) имеет место тогда и только тогда, когда любой простой элемент 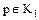 , делящий произведение
, делящий произведение 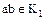 , делит по крайней мере один из сомножителей
, делит по крайней мере один из сомножителей  или
или 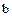 .
.
Доказательство. Пусть 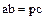 . Если
. Если
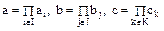
разложения 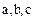 на простые множители, а
на простые множители, а  – кольцо с однозначным разложением, то из равенств
– кольцо с однозначным разложением, то из равенств 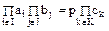 следует, что элемент
следует, что элемент  ассоциирован с одним из
ассоциирован с одним из 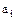 или
или 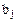 , т.е.
, т.е.  делит
делит  или
или 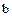 .
.
Обратно, установим однозначность разложения в  , где
, где 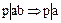 или
или 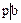 . Рассуждая по индукции, допустим, что разложение всех элементов из
. Рассуждая по индукции, допустим, что разложение всех элементов из  с числом
с числом 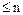 простых множителей единственно (с точностью до порядка сомножителей и их ассоциированности).
простых множителей единственно (с точностью до порядка сомножителей и их ассоциированности).
Докажем теперь это для любого элемента 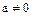 , который может быть разложен на
, который может быть разложен на 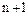 простых сомножителей. Именно, пусть
простых сомножителей. Именно, пусть
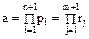 (47)
(47)
– два разложения элемента  с
с 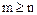 .
.
Условие теоремы, примененное к 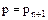 дает нам, что
дает нам, что 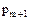 должен делить один из элементов
должен делить один из элементов 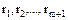 . Без ограничения общности (это вопрос нумерации) будем считать, что
. Без ограничения общности (это вопрос нумерации) будем считать, что 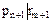 . Но
. Но 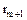 – простой элемент, поэтому
– простой элемент, поэтому 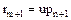 , где
, где 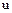 – обратимый элемент. Используя закон сокращения в
– обратимый элемент. Используя закон сокращения в  , получаем из (41) равенство
, получаем из (41) равенство
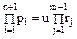 . (48)
. (48)
В левой части равенства (42) стоит произведение 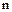 простых сомножителей. По предположению индукции
простых сомножителей. По предположению индукции 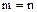 и оба разложения отличаются лишь порядком простых элементов, снабженных, возможно, какими–то обратимыми сомножителями.
и оба разложения отличаются лишь порядком простых элементов, снабженных, возможно, какими–то обратимыми сомножителями.
Замечание. В произвольном кольце целостности  элемент
элемент 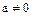 вообще не обязан допускать разложение типа (40). Более интересным является тот факт, что имеются кольца целостности, в которых разложение на простые множители хотя и возможно, но не является однозначным, т.е. условия теоремы, кажущиеся тривиальными не всегда выполняются.
вообще не обязан допускать разложение типа (40). Более интересным является тот факт, что имеются кольца целостности, в которых разложение на простые множители хотя и возможно, но не является однозначным, т.е. условия теоремы, кажущиеся тривиальными не всегда выполняются.
Пример. Рассмотрим кольцо целостности 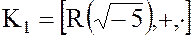 , где
, где 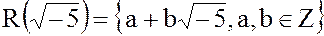 .
.
Норма 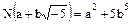 каждого отличного от нуля элемента
каждого отличного от нуля элемента 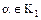 – целое положительное число. Если элемент
– целое положительное число. Если элемент 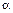 обратим в
обратим в  , то
, то 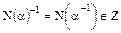 , откуда
, откуда 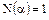 . Это возможно лишь при
. Это возможно лишь при 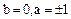 . Таким образом в
. Таким образом в  , как и в 1
, как и в 1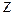 , обратимыми элементами являются только
, обратимыми элементами являются только 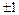 . Если
. Если 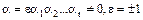 , то
, то 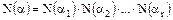 . Так как
. Так как 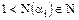 , то при заданном
, то при заданном 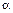 число множителей
число множителей 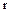 не может неограниченно расти. Следовательно, разложение на простые множители в
не может неограниченно расти. Следовательно, разложение на простые множители в  возможно. Вместе с тем число 9 (да и не только оно) допускает два существенно различных разложения на простые множители:
возможно. Вместе с тем число 9 (да и не только оно) допускает два существенно различных разложения на простые множители:
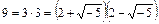 .
.
Неассоциированность элементов 3 и 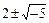 очевидна. Далее,
очевидна. Далее, 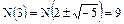 . Поэтому из разложения
. Поэтому из разложения 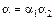 для
для 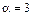 или
или 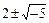 с необратимыми
с необратимыми 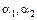 следовало бы
следовало бы 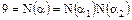 , т.е.
, т.е. 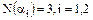 , что невозможно, поскольку уравнение
, что невозможно, поскольку уравнение 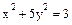 с
с 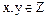 неразрешимо. Этим доказана простота элементов 3 и
неразрешимо. Этим доказана простота элементов 3 и 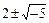 .
.
 2014-02-13
2014-02-13 2663
2663