Рассмотрим некоторые элементарные операции над идеалами кольца 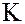 . Пусть
. Пусть 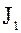 и
и 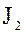 два произвольных идеала кольца
два произвольных идеала кольца 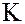 .
.
Теорема. Пересечение  идеалов
идеалов 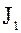 и
и 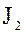 кольца
кольца 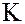 является идеалом этого кольца.
является идеалом этого кольца.
Доказательство. Пересечение идеалов  является подгруппой аддитивной группы кольца
является подгруппой аддитивной группы кольца 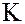 . Кроме того, для любых элементов
. Кроме того, для любых элементов 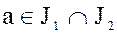 и
и 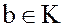 произведение
произведение 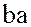 и
и 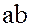 содержится в идеалах
содержится в идеалах 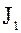 и
и 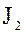 и, следовательно, содержится и в их пересечении
и, следовательно, содержится и в их пересечении  . Следовательно, пересечение идеалов
. Следовательно, пересечение идеалов  является идеалом кольца
является идеалом кольца 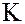 .
.
Замечание. 1. Можно показать, что операция пересечения идеалов ассоциативна и коммутативна.
2. Рассмотренная теорема легко распространяется на любое конечное или счетное число идеалов.
Пусть 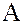 и
и 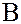 – некоторые не пустые подмножества кольца
– некоторые не пустые подмножества кольца 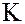 .
.
Определение. Множество всех элементов вида 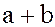 , где
, где 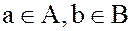 называется суммой подмножеств
называется суммой подмножеств 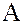 и
и 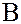 и обозначается символом
и обозначается символом 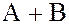 :
:
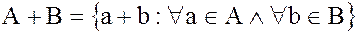 . (3.66)
. (3.66)
Если подмножество 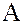 состоит только из одного элемента
состоит только из одного элемента 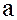 , то сумма
, то сумма 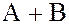 обозначается
обозначается 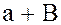 .
.
Определение. Произведением 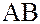 подмножеств
подмножеств 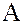 и
и 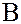 называется множество всех элементов вида:
называется множество всех элементов вида:
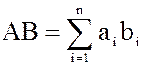 , (3.67)
, (3.67)
где 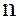 – некоторое натуральное число,
– некоторое натуральное число, 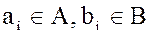 .
.
Если подмножество 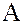 состоит только из одного элемента
состоит только из одного элемента 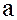 , то произведение
, то произведение 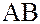 обозначают символом
обозначают символом 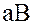 . Это произведение состоит из всех элементов вида
. Это произведение состоит из всех элементов вида 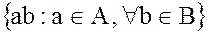 .
.
Замечание. Определенная таким образом операция умножения подмножеств кольца 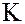 ассоциативна. Если кольцо
ассоциативна. Если кольцо 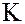 коммутативное, то операция умножения подмножеств также будет коммутативной.
коммутативное, то операция умножения подмножеств также будет коммутативной.
Пусть 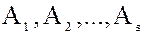 – подмножества кольца
– подмножества кольца 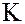 , тогда их произведение
, тогда их произведение
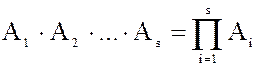 , (3.68)
, (3.68)
состоит из всех сумм произведений вида 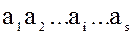 , где
, где 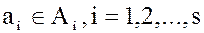 .
.
Применим введение операции сложения и умножения подмножеств кольца 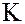 к его идеалам
к его идеалам 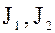 .
.
Теорема. Сумма 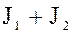 идеалов
идеалов 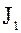 и
и 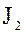 кольца
кольца 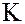 является идеалом этого кольца.
является идеалом этого кольца.
Доказательство. Пусть 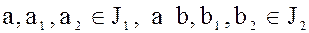 , тогда сумма
, тогда сумма 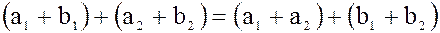 любых двух элементов
любых двух элементов 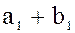 и
и 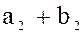 множества
множества 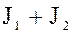 принадлежит к
принадлежит к 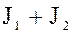 , поскольку
, поскольку 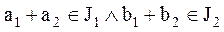 и элемент
и элемент 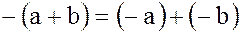 , противоположный произвольного выбранному элементу
, противоположный произвольного выбранному элементу 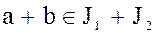 , также принадлежит к
, также принадлежит к 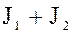 , так как
, так как 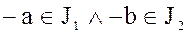 . Следовательно,
. Следовательно, 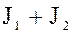 является подгруппой аддитивной группы кольца
является подгруппой аддитивной группы кольца 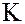 . Кроме того, для любых элементов
. Кроме того, для любых элементов 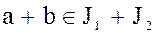 и любого
и любого 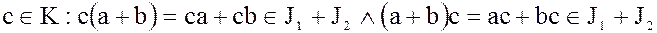 .
.
Теорема. Произведение 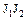 идеалов
идеалов 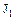 и
и 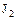 кольца
кольца  также является идеалом кольца
также является идеалом кольца  .
.
Доказательство. Действительно, сумма 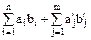 любых двух элементов
любых двух элементов 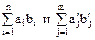 множества
множества 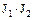 является, очевидно, элементом этого же множества, а элемент
является, очевидно, элементом этого же множества, а элемент 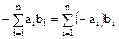 – противоположный произвольно выбранному элементу
– противоположный произвольно выбранному элементу 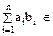
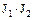 , принадлежит к
, принадлежит к 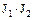 . Кроме того для любых
. Кроме того для любых 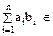
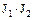 и
и 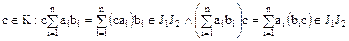 .
.
Таким образом, в множестве идеалов кольца  выполнимы операции сложения и умножения. Операция сложения идеалов – ассоциативна и коммутативна, а операция умножения – ассоциативна. Если кольцо
выполнимы операции сложения и умножения. Операция сложения идеалов – ассоциативна и коммутативна, а операция умножения – ассоциативна. Если кольцо  – коммутативное, то операция умножения идеалов также коммутативна.
– коммутативное, то операция умножения идеалов также коммутативна.
Теорема. Операции сложения и умножения идеалов 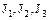 кольца
кольца  связаны дистрибутивными законами
связаны дистрибутивными законами
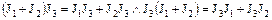 .
.
Справедливость этого утверждения очевидна.
Теорема. Ядро гомоморфизма колец 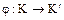
 ,является идеалом в кольце
,является идеалом в кольце 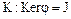 кольца
кольца  .
.
Доказательство. 1. Пусть G группа в K, а 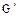 группа в
группа в 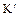 . Тогда используя теорему о ядре гомоморфизма групп получаем, что если
. Тогда используя теорему о ядре гомоморфизма групп получаем, что если  , то
, то 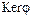 – подгруппа в
– подгруппа в 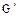 и, следовательно,
и, следовательно, 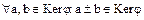 т.е. условие (3.39) теоремы выполнено.
т.е. условие (3.39) теоремы выполнено.
Пусть 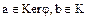 для выполнения условия (3.40) необходимо доказать, что
для выполнения условия (3.40) необходимо доказать, что  . Покажем, что
. Покажем, что 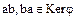 . Действительно, из свойств гомоморфизма колец имеем:
. Действительно, из свойств гомоморфизма колец имеем:
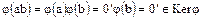 ,
,
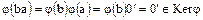 .
.
 2014-02-13
2014-02-13 3922
3922
