Среди подколец особую роль играют подкольца, называемые идеалами: их роль аналогична роли нормальных делителей в теории групп.
Определение. Непустое подмножество 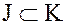 кольца
кольца  называется идеалом кольца
называется идеалом кольца  , если выполняются два условия:
, если выполняются два условия:
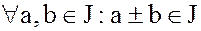 , (7)
, (7)
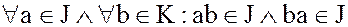 . (8)
. (8)
Эти условия означают, что идеал - это аддитивная подгруппа в кольце K, а операция умножения в кольце коммутативна.
Пример. Рассмотрим кольцо целых чисел 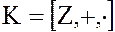
и кольцо целых чисел, делящихся на 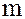 без остатка,
без остатка, 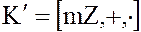 .
.
Ясно, что 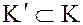 .
.
Покажем, что 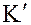 – идеал.
– идеал.
Действительно,
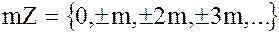 .
.
Проверим выполнение условия (7). Пусть
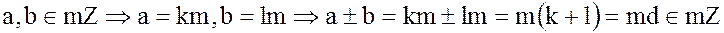 ,
,
где 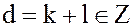 .
.
Проверим выполнение условия (8). Пусть
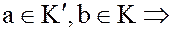
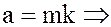
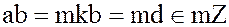 , где
, где 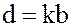 .
.
Обратно, 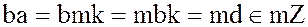 .
.
Следовательно, 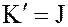 – идеал кольца
– идеал кольца  .
.
Каждое коммутативное кольцо  , очевидно, является своим идеалом. Этот идеал называют единичным
, очевидно, является своим идеалом. Этот идеал называют единичным 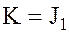 .
.
В каждом кольце 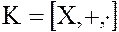 нулевое подкольцо
нулевое подкольцо 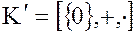 является идеалом, его называют нулевым идеалом и обозначают символом
является идеалом, его называют нулевым идеалом и обозначают символом 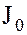 .
.
Единичный идеал 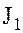 кольца
кольца  содержит все элементы кольца, т.е. совпадает с самим кольцом
содержит все элементы кольца, т.е. совпадает с самим кольцом 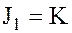 и, следовательно, содержит любой идеал
и, следовательно, содержит любой идеал 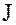 этого кольца, а нулевой идеал
этого кольца, а нулевой идеал 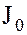 содержится в каждом идеале
содержится в каждом идеале 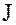 кольца
кольца  .
.
Следовательно, в смысле отношения включения, единичный идеал – самый большой, а нулевой – самый меньший среди всех идеалов кольца.
Рассмотрим понятие идеала 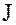 кольца более детально.
кольца более детально.
Пусть  – некоторое кольцо, и
– некоторое кольцо, и 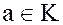 – любой элемент этого кольца.
– любой элемент этого кольца.
Определение. Множество 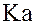 всех элементов вида:
всех элементов вида:
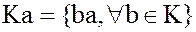
называется левым идеалом; а множество
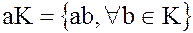
называется правым идеалом, а множество
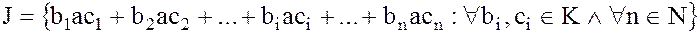
называется двусторонним идеалом кольца  .
.
Покажем, что множество 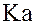 является левым идеалом кольца
является левым идеалом кольца  . Сумма любых двух элементов
. Сумма любых двух элементов 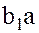 и
и 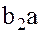 множества
множества 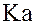 принадлежит этому самому множеству:
принадлежит этому самому множеству:

т.к. 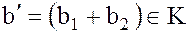 .
.
Для любого элемента 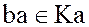 противоположный элемент
противоположный элемент 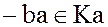 :
:
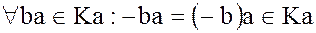 , т.к.
, т.к. 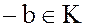 .
.
Поэтому множество 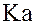 является подгруппой аддитивной группы кольца
является подгруппой аддитивной группы кольца  .
.
Для любых элементов 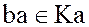 и
и 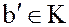 произведение
произведение 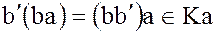 .
.
Следовательно, 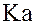 – левый идеал кольца
– левый идеал кольца  .
.
Аналогично доказывается, что 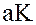 – правый, а
– правый, а 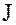 – двусторонний идеал кольца
– двусторонний идеал кольца  . Если
. Если  – коммутативное кольцо, то
– коммутативное кольцо, то 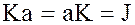 .
.
Замечание. Если кольцо  не содержит единицы, то каждый из идеалов
не содержит единицы, то каждый из идеалов 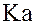 ,
, 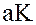 ,
, 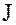 может не содержать элемента
может не содержать элемента 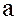 .
.
Если задано некоторое кольцо  , то естественно, возникает вопрос: как построить или получить идеал этого кольца
, то естественно, возникает вопрос: как построить или получить идеал этого кольца  ?
?
Вначале рассмотрим построение идеала для некоммутативных колец.
Пусть  – некоторое некоммутативное кольцо и
– некоторое некоммутативное кольцо и 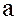 – любой фиксированный элемент этого кольца.
– любой фиксированный элемент этого кольца.
Теорема. Множество элементов вида
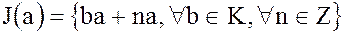
где 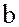 – любой элемент кольца
– любой элемент кольца  , а
, а 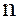 – любое целое число, является идеалом кольца
– любое целое число, является идеалом кольца  .
.
Этот идеал называется главным идеалом кольца, порожденным элементом 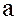 , и обозначается символом
, и обозначается символом 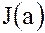 .
.
Среди идеалов, которые содержат элемент 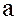 , главный идеал
, главный идеал 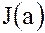 является наименьшим (в смысле отношения включения).
является наименьшим (в смысле отношения включения).
Доказательство. Действительно, каждый идеал, который содержит элемент 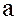 , содержит все кратные
, содержит все кратные 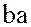 и все суммы
и все суммы 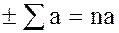 , а следовательно, и все суммы
, а следовательно, и все суммы 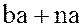 , т.е. содержит идеал
, т.е. содержит идеал 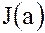 .
.
Теорема. (о идеале коммутативного кольца) В коммутативном кольце K множество
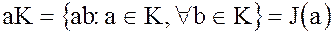
является идеалом в K. Этот идеал называется главным идеалом, порожденным элементом 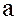 и обозначается
и обозначается 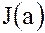 .
.
Доказательство. В коммутативном кольце
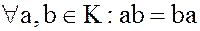 .
.
Докажем первое свойство идеала, т.е. если
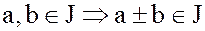 ,
,
в данном случае роль 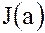 играет
играет 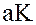 , т.е.
, т.е. 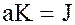 .
.
Пусть
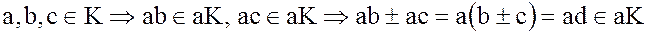 ,
,
т.к. 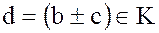 .
.
Докажем второе свойство идеала
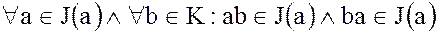 ,
,
где, как и ранее, 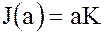 .
.
Пусть
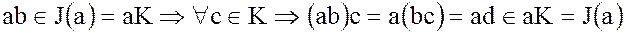 ,
,
с другой стороны 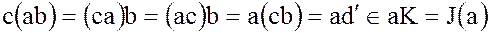 .
.
Определение. Кольцо  , в котором все идеалы главные, называется кольцом главных идеалов.
, в котором все идеалы главные, называется кольцом главных идеалов.
Если в кольце  есть единица
есть единица 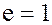 , то
, то 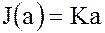 .
.
Действительно, из определения идеала 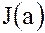 следует, что
следует, что 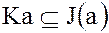 .
.
С другой стороны,
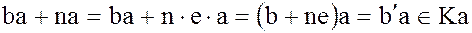 ,
,
поэтому 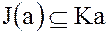 .
.
Следовательно, 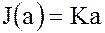 .
.
Например, главный идеал 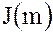 кольца целых чисел
кольца целых чисел 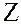 состоит из всех целых чисел, кратных числу
состоит из всех целых чисел, кратных числу 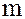 :
:
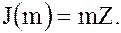
Замечание. Нулевой идеал 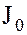 кольца
кольца  является главным идеалом
является главным идеалом 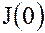 . Если в кольце есть единица
. Если в кольце есть единица 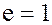 , то единичный идеал
, то единичный идеал 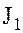 кольца
кольца  также является идеалом
также является идеалом 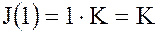 .
.
Аналогично тому, как мы определили понятие главного идеала 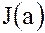 коммутативного кольца
коммутативного кольца  , можно определить понятие идеала, порожденного несколькими элементами
, можно определить понятие идеала, порожденного несколькими элементами 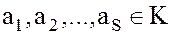 .
.
Пусть  – некоторое коммутативное кольцо и пусть
– некоторое коммутативное кольцо и пусть 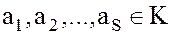 .
.
Множество элементов вида:
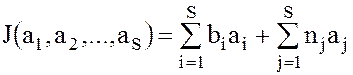 ,
,
где 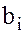 – любой элемент из кольца
– любой элемент из кольца  ,
, 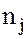 – любое целое число, является идеалом кольца
– любое целое число, является идеалом кольца  .
.
Множество элементов 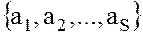 называется базисом идеала
называется базисом идеала 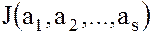 кольца
кольца  .
.
Замечание. Для идеала 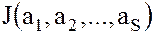 , кроме базиса
, кроме базиса 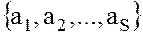 могут существовать и другие базисы, причем некоторые из них могут состоять из меньшего, чем
могут существовать и другие базисы, причем некоторые из них могут состоять из меньшего, чем 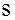 , числа элементов.
, числа элементов.
 2014-02-13
2014-02-13 7662
7662








