ЛЕКЦИЯ 16
Пусть 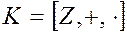 – кольцо целых чисел, а
– кольцо целых чисел, а 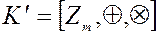 – кольцо классов вычетов по модулю
– кольцо классов вычетов по модулю 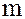 . Рассмотрим отображение
. Рассмотрим отображение
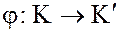 , (1)
, (1)
определяемое как
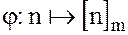 , (2)
, (2)
где 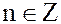 ,
, 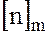 – класс вычетов по
– класс вычетов по 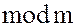 , в который попадает число
, в который попадает число 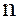 .
.
Таких классов ровно 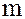 и отображение
и отображение 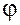 – сюрьективно.
– сюрьективно.
Пусть 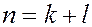 , где
, где 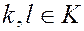 , тогда в силу определенных в кольце
, тогда в силу определенных в кольце 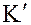 операций сложения
операций сложения 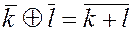 и умножения
и умножения 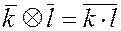 имеем:
имеем:
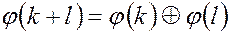 , (3)
, (3)
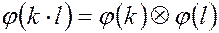 , (4)
, (4)
что позволяет говорить о гомоморфизме колец  и
и 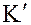 .
.
Обобщим этот факт в виде следующего определения.
Определение. Пусть 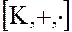 и
и 
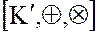 два кольца. Отображение
два кольца. Отображение 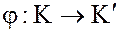 называется гомоморфизмом, если оно сохраняет операции
называется гомоморфизмом, если оно сохраняет операции
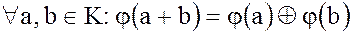 , (5)
, (5)
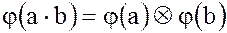 , (6)
, (6)
где 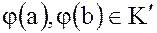 .
.
Чтобы указать, что
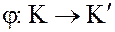 – гомоморфное отображение кольца
– гомоморфное отображение кольца  на кольцо
на кольцо 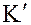 пишут
пишут 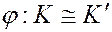 или Hom:
или Hom: 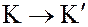 .
.
Пример. Пусть 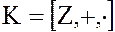 – кольцо целых чисел,
– кольцо целых чисел, 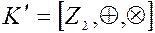 – кольцо классов вычетов по модулю 2.
– кольцо классов вычетов по модулю 2.
Кольцо 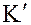 – содержит два класса:
– содержит два класса:
класс четных чисел – 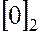
класс нечетных чисел 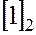 .
.
Отображениe
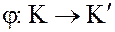 ,
, 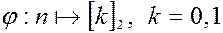 ,
,
которое каждому четному числу 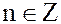 ставит в соответствие класс
ставит в соответствие класс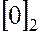 , а каждому нечетному – класс
, а каждому нечетному – класс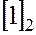 , является гомоморфизмом.
, является гомоморфизмом.
Рассмотрим основные свойства гомоморфных отображений колец, которые сформулируем в виде следующей теоремы.
Теорема. Если 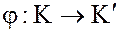 гомоморфизм кольца
гомоморфизм кольца  в кольцо
в кольцо 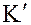 , то:
, то:
1.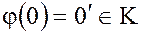 (нуль кольца K отображается в нуль кольца
(нуль кольца K отображается в нуль кольца 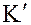 );
);
2.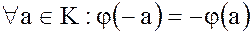 ;
;
3. 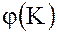 есть подкольцо кольца
есть подкольцо кольца 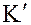 :
:
4. Если для операции умножения в 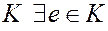 , то
, то 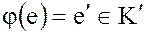 , а если для
, а если для 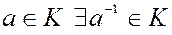 , то
, то 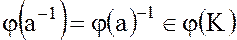 .
.
Доказательство.
1. Если 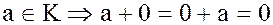 .
.
Тогда
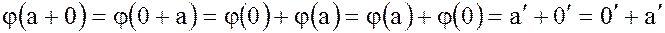 ,
,
где 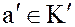 .
.
Отсюда следует, что 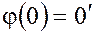 – есть нулевой элемент кольца
– есть нулевой элемент кольца 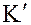 .
.
2. Докажем, что для 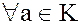 :
: 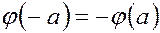 .
.
Действительно, 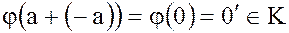 .
.
С другой стороны, 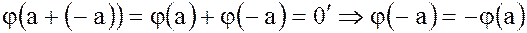 .
.
3. Докажем, что 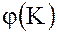 – подкольцо кольца
– подкольцо кольца 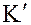 .
.
Утверждение будет доказано, если мы покажем, что:
а.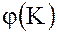 – группа по сложению,
– группа по сложению,
б.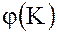 – полугруппа по умножению.
– полугруппа по умножению.
А) Пусть
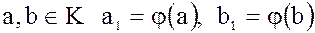 ,
,
т.е. 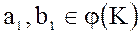 - два произвольных элемента
- два произвольных элемента 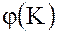 , тогда
, тогда
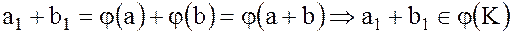 ,
,
следовательно 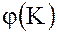 – подгруппа в
– подгруппа в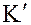 .
.
Б.) Покажем, что если 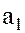 и
и 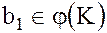 , то и их произведение
, то и их произведение 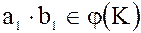 .
.
Действительно, если 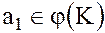 и
и 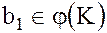 , то
, то
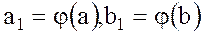 , где
, где 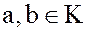 .
.
Тогда 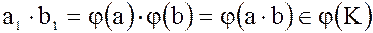 .
.
4. Докажем, что
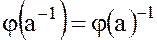 .
.
Действительно, если 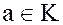 и
и
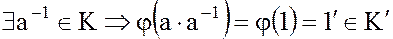 .
.
С другой стороны, т.к. 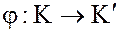 – гомоморфизм, то
– гомоморфизм, то
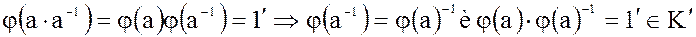 .
.
Замечание. Если 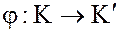 – гомоморфизм колец, то для любого фиксированного
– гомоморфизм колец, то для любого фиксированного
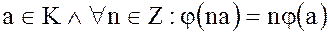 .
.
Действительно, пусть 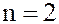 , тогда
, тогда
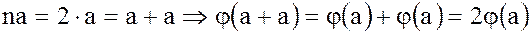 .
.
Вместе с тем, выражение 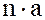 не следует рассматривать как настоящее произведение двух элементов кольца, потому что в общем случае
не следует рассматривать как настоящее произведение двух элементов кольца, потому что в общем случае 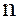 не является элементом кольца, а представляет собой нечто внешнее – целое число.
не является элементом кольца, а представляет собой нечто внешнее – целое число.
Однако, если кольцо обладает единицей 1, то  можно рассматривать как настоящее произведение, а именно
можно рассматривать как настоящее произведение, а именно
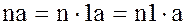 .
.
Аналогично морфизмам групп, рассматриваются морфизмы колец, при этом гомоморфизм 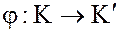 называется:
называется:
– мономорфизмом, если отображение 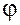 – инъективно:
– инъективно:
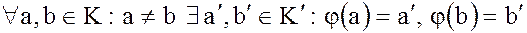 ,
, 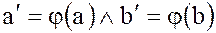
причем 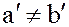 , т.е. образы различных элементов различны.
, т.е. образы различных элементов различны.
– эпиморфизмом, если 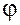 – сюрьективно:
– сюрьективно:
каждый элемент 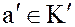 имеет прообраз
имеет прообраз 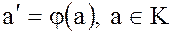 т.е.
т.е.
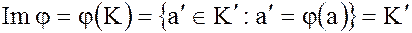 ;
;
– изоморфизмом, если 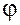 – биективно.
– биективно.
Факт изоморфизма колец кратко записывается в виде 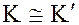 .
.
Пример. Пусть 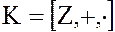 – кольцо целых чисел, а
– кольцо целых чисел, а 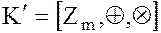 – кольцо классов вычетов по модулю
– кольцо классов вычетов по модулю 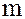 .
.
Рассмотрим отображение
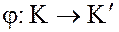 ,
,
такое, что
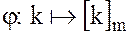 .
.
1. Отображение 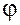 является гомоморфизмом, т.к. сохраняет групповые операции:
является гомоморфизмом, т.к. сохраняет групповые операции:
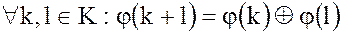
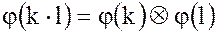
Для классов вычетов эти операции имеют вид:
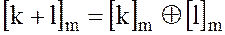
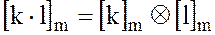
2. Отображение 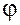 является эпиморфизмом,
является эпиморфизмом,
т.е. 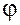 – сюрьективно для любого
– сюрьективно для любого 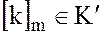 имеется прообраз
имеется прообраз  , такой, что
, такой, что
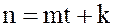 ,
,
т.е. при делении на 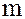 число
число 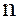 дает положительный остаток равный
дает положительный остаток равный 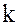 ;
;
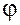 – не инъективно, т.к. если, как и ранее
– не инъективно, т.к. если, как и ранее 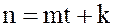 , то
, то 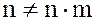 имеют один и тот же образ
имеют один и тот же образ 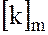 .
.
Ядро гомоморфизма колец
Определение. Ядром гомоморфизма колец 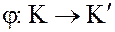 называется множество
называется множество
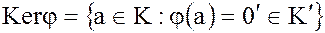
На рисунке 1 заштрихованной областью изображено ядро гомоморфизма колец  и
и 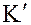 .
.
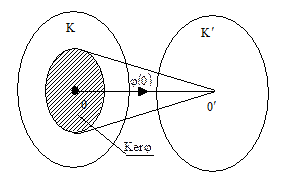
Рис. 1 – Ядро гомоморфизма колец 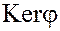 .
.
Ясно, что 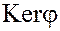 – подкольцо кольца
– подкольцо кольца  , но это особое подкольцо.
, но это особое подкольцо.
Напомним, что если K – некоторое кольцо, то для того, чтобы непустое подмножество 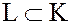 было кольцом (подкольцом K), необходимо и достаточно, чтобы выполнялись следующие условия:
было кольцом (подкольцом K), необходимо и достаточно, чтобы выполнялись следующие условия:
1. L – должно быть подгруппой аддитивной группы кольца K, т.е.
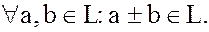
2. L – должно быть замкнуто относительно операции умноження, т.е.
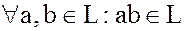 .
.
 2014-02-13
2014-02-13 3567
3567







