Фактор-кольцо

Понятие идеала 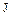кольца 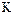аналогично понятию нормального делителя H для группы G. Это позволяет подойти к построению фактор-кольца 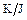таким же образом как и при построении фактор-группы G/H. Пусть 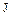– идеал кольца 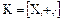. Так как. основу кольца 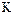составляет аддитивная абелева группа 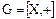, поэтому в качестве элементов фактор-кольца можно выбрать смежные классы 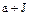, где 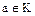, которые называются классами вычетов по модулю идеала кольца.

Теорема. Множество аддитивных смежных классов 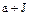образуют фактор-кольцо 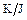с операциями:

1. 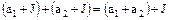(3.70)

2. 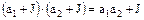(3.71)

Кроме того, естественное отображение 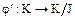вида 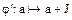, является эпиморфизмом (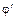– сюрьективно).

Доказательство. В абелевой группе 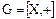любая подгруппа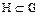нормальна т.к. 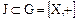поэтому выражение (3.69) определяет абелеву группу фактор-кольца 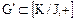, а отображение 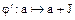является эпиморфизмом аддитивных абелевых групп G и 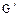. Остается проверить, что выражение (3.70) однозначно определяет операцию умножения на множестве аддитивных смежных классов 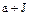т.е. не зависит от выбора представителей соответствующих классов.

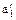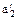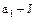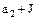Пусть ,представители двух смежных классов , и т.е. 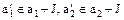, тогда 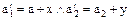где .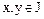

Найдем произведение

,

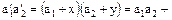
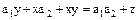где .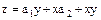

Остается показать, что 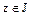. Действительно, т.к. 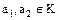и 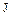– идеал в K, то 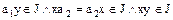т.к. .

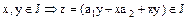Поэтому 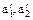находятся в одном смежном классе с элементами 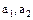, а это означает что произведение (3.51) определено правильно.

Пример. Рассмотрим кольцо целых чисел 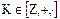. Идеалом этого кольца является 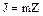т.е. множество целых чисел, делящихся на m без остатка.

Аддитивный смежный класс кольца K по идеалу 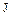имеет вид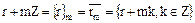, где .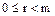

Множество аддитивных смежных классов содержит ровно 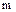классов вычетов по модулю 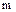, и они имеют вид:

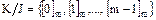
Таким образом, элементами фактор-кольца 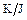являются классы вычетов по модулю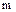 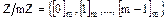. Операции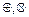, на фактор-кольце 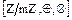задаются на классах вычетов как и ранее:

,

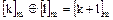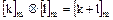
При фиксированном m будем, как и ранее, использовать сокращенные записи :

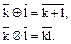
Понятие фактор-кольца 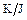по идеалу кольца 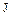позволяет сформировать основную теорему о гомоморфизме колец.

Теорема (о гомоморфизме колец). Пусть 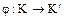– гомоморфизм кольца 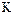на кольцо 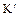, 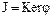. Тогда кольцо 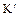изоморфно фактор-кольцу 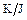, причем изоморфизм может быть выбран так, что 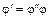т.е. для всех 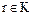имеем , где 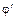– естественный гомоморфизм кольца 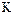на фактор-кольцо 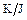. Другими словами, теорема утверждает, что диаграмма

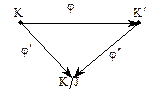
коммутативна, т.е. .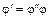

Доказательство. Пусть 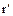– произвольный элемент кольца 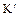, и 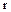– некоторый элемент кольца 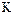, такой, что . Тогда 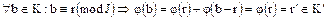, поскольку 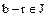, следовательно, . С другой стороны, если элемент 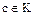при гомоморфизме 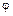отображается в элемент 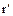, т.е. 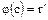, то 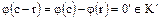, и поэтому 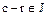, т.е. 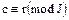. Следовательно, множество всех элементов кольца 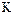, которые при гомоморфизме 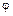отображаются в элемент 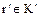, является классом вычетов кольца 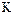по модулю 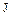, к которому принадлежит элемент 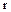, т.е. классом .

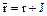Обозначим символом 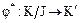отображение фактор-множества (множества классов вычетов по модулю 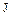) 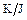в 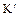, которое каждому классу вычетов 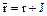ставит в соответствие элемент 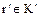, в который при гомоморфизие 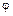отображаются все элементы класса 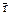, т.е. 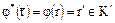, где 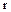– любой элемент из класса вычетов 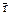. Очевидно, что 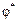является сюрьективным отображением фактор-кольца 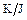на кольцо 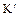. Отображение 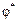является гомоморфизмом. Действительно, пусть 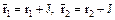– два произвольно выбранных элемента кольца 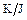. 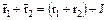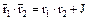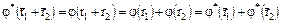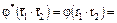Тогда , и поэтому , , 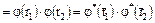т.е. .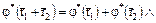

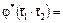
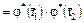Докажем теперь, что отображение 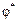инъективно т.е. образы различных элементов различны. Действительно, если 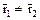, то 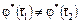. Это действительно так. Если 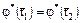, то по определению 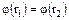т.е. 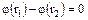. Поэтому 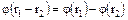и 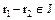. Отсюда 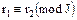и 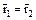. Следовательно, 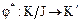является изоморфизмом (биективным гомоморфизмом) фактор-кольца 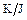на кольцо 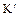. Это означает, что существует обратное отображение 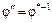: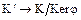,которое также является изоморфизмом кольца 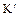на фактор-кольцо 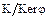. Рассмотрим теперь отображение . 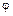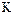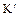Поскольку – гомоморфизм колльца на , а 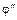– изоморфизм кольца 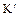на фактор-кольцо 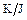, то композиция отображений 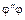определяет отображение кольца 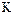на фактор-кольцо 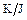. Докажем теперь, что 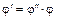. Пусть 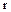– произвольный элемент кольца 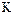. По определению естественного отображения 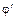, 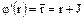. С другой стороны по определению гомоморфизма 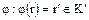. 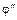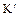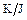Учитывая, что – изоморфизм на имеем . Следовательно . 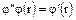Таким образом 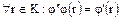, а это означает, что 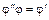, что и требовалось доказать.

Замечание. Теорема о гомоморфизмах колец доказывает, что естественными гомоморфизмами кольца 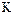на его фактор-кольцо по двухстороннему идеалу 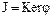по существу исчерпываются все его гомоморфизмы.