2014-02-13
549
Метод планов положений, скоростей и ускорений (графоаналитический метод)
Задача о вторых передаточных функциях механизма.
Задача о положениях звеньев механизма
Проецируем векторный контур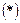 
на оси координат и получаем координаты точки С механизма:
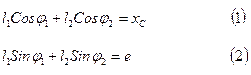
из решения этой системы уравнений определяем неизвестные величины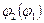 
и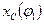 
, которые определяют положение звеньев и точек механизма в зависимости от обобщенной координаты.
Учитывая, что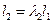 
, а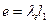 
из (2) найдем 
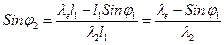, т.к. угол 
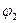может лежать только в I и IV четвертях, то из последнего выражения можно найти 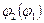с учетом знака, если 
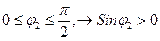, если 
:
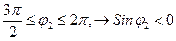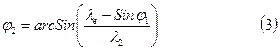
Учитывая основное тригонометрическое тождество, найдем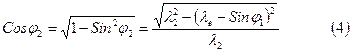 
,
из (1) с учетом :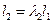
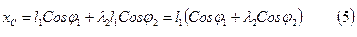Проецируем векторный контур 
на оси координат и получаем координаты точки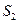 
механизма:
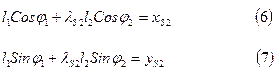
С учетом ,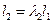
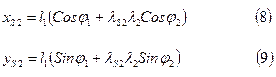
Таким образом, мы нашли функции всех положений (3), (5), (8) и (9).
1. 2. Задача о первых кинематических передаточных функциях механизма
Продифференцируем уравнения проекций векторного контура по обобщенной координате и получим
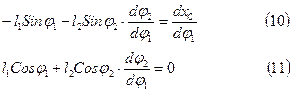
Из этой системы уравнений определяем первые передаточные функции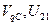 
.
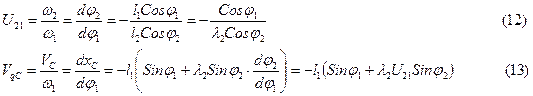
Продифференцируем уравнения проекций векторного контура по обобщенной координате и получим
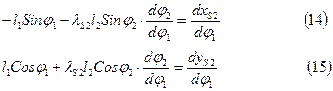
Из этой системы уравнений определяем первые передаточные функции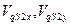 
.
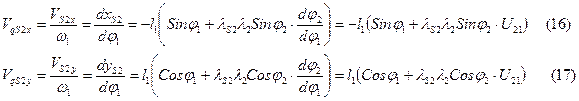
Откуда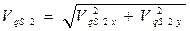 
Вторично продифференцируем уравнения проекций векторного контура 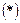по обобщенной координате и получим
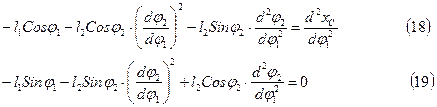
Из этой системы уравнений определяем вторые передаточные функции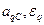 
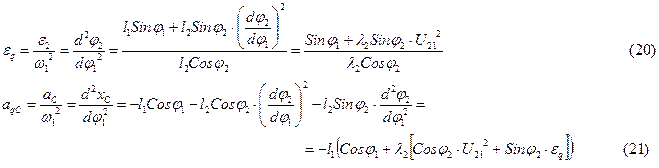Вторично продифференцировав уравнения проекций векторного контура 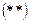по обобщенной координате, получим 
.
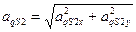Таким образом, очевидно, что аналитический метод сводится только к умению грамотно дифференцировать, а потому чрезвычайно удобен при применении ПЭВМ. Полученные формулы позволяют создать цикл с переменной обобщенной координатой, и как следствие получить значения всех передаточных функций в виде таблицы значений или кинематических диаграмм.
При использовании этого метода необходимо иметь схему механизма, а также уметь грамотно строить планы скоростей и ускорений.
Определим передаточные функции первого порядка также для кривошипно-ползунного механизма.
Планом механизма называется изображение кинематической схемы механизма в выбранном масштабе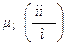 
соответствующее определенному положению ведущего звена.
Масштабом называется величина равная отношению длины отрезка в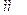 
на чертеже к величине физической в единицах измерения СИ.
План скоростей и план ускорений – это графическое изображение векторных уравнений, связывающих скорости и ускорения всех точек звеньев механизма.
Метод подобия: точки, принадлежащие одному звену механизма, и концы векторов скоростей этих точек на плане скоростей образуют подобные фигуры (прямые, треугольники и пр.), при этом вектора скоростей этих точек начинаются в полюсе и направление обхода точек должно совпадать с направлением обхода для соответствующего звена механизма. Метод подобия применим и для плана ускорения.
Пример. Заданы размеры механизма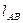 
, 
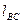; положение механизма, определяемое 
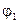; кинематические параметры 
, 
.
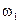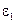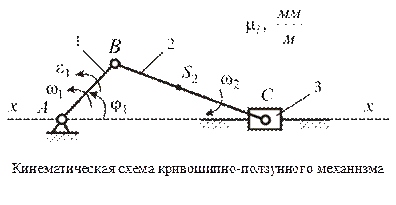
Строится план механизма в масштабе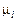 
.
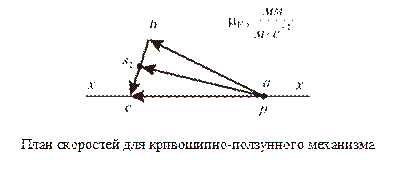
Строится план скоростей в масштабе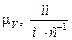 
на основании векторных уравнений, связывающих скорости всех точек звеньев механизма.
Звено 1 совершает вращательное движение, звено 2 – плоскопараллельное, звено 3 – поступательное.
| 
|
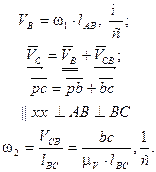
Используя метод подобия, определяется положение точки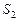 
:
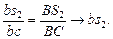
Все вектора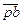 
, 
, 
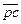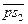абсолютных скоростей 
, 
, 
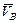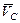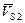выходят из полюса 
.
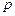Аналог скорости точки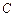 
: 
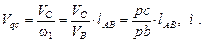
Передаточное отношение для 2 звена: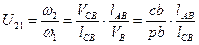 
.
Это графическое равенство можно поострить без выбора масштаба скоростей (если не стоит задача определения передаточных функций ускорений), так как передаточные функции определяются только отношением отрезков и не зависят от угловой скорости входного звена.
Центроидой (полоидой) называется геометрическое место центров (полюсов) относительного вращения в системах координат связанных со звеньями механизма. В зубчатом механизме при передаче движения центроиды колес перекатываются друг по другу без скольжения. На основании этого выводится основная теорема зацепления Виллиса, с которой мы познакомимся позднее.
