2014-02-13
3971
Заметим, что указанные выше условия сходимости для простой итерации остается верной для итерации по методу Зейделя. Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации, но приводит к более громоздким вычислениям.
Метод Зейделя представляет собой некоторую модификацию метода итераций. Основная его идея заключается в том, что при вычислении (k + 1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k + 1)-е приближения неизвестных x1, x2, …, xi - 1.
.
Метод Зейделя
Пусть получена эквивалентная система (18). Выберем произвольно начальные приближения корней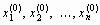 
. Далее, предполагая, что k -ые приближения 
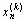корней известны, согласно Зейделю будем строить (k + 1)-е приближения корней по формулам:
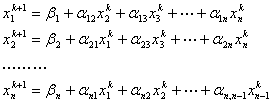 | (22) |
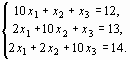
Приведем эту систему к виду, удобному для итерации:
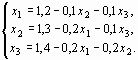
В качестве нулевых приближений корней возьмем: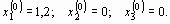 
Применяя процесс Зейделя, последовательно получим:
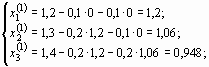
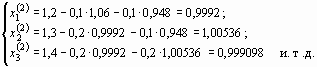
Результаты вычислений с точностью до четырех знаков приведены в таблице ниже:
