Возвращает норму матрицы А (по строкам)

.

.

Пусть

Или

Или

Теорема: Процесс итерации для приведенной линейной системы (18) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы a меньше единицы, т.е. для итерационного процесса (19) достаточное условие есть

Приведем достаточное условие сходимости метода итераций.

А любое (k + 1) приближение вычисляется по формуле

Систему (18) можно записать в матричной форме

Введя матрицы

При i не равно j

Где

и a _ij = 0 при i = j (i, j = 1, 2, …, n).

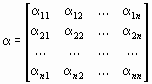и ,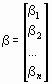

x = b + a x,

x (k+1) = b + a x (k).

Напишем формулы приближений в развернутом виде:

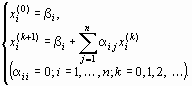
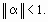
Следствие 1. Процесс итерации для системы (18) сходится, если:

1) 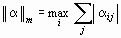< 1 (m- норма или неопределенная норма)

2) 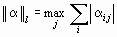< 1 (l- норма или норма L 1)

3) 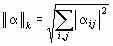< 1 (k- норма или Евклидова норма).

Следствие 2. Для системы (13) процесс итерации сходится, если выполнены неравенства:

1. 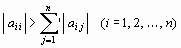или 2. ,

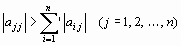где штрих у знака суммы означает, что при суммировании пропускаются значения i = j, т. е. сходимость имеет место, если модули диагональных элементов матрицы А системы (13) или для каждой строки превышают сумму модулей недиагональных элементов этой строки, или же для каждого столбца превышают сумму модулей недиагональных элементов этого столбца.

Имеем:

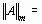max(1+ 2 + 3, 4 + 5 + 6, 7 + 8 + 9) = max (6, 15, 24) = 24;

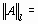max(1+ 4 + 7, 2 + 5 + 8, 3 + 6 + 9) = max (12, 15, 18) = 18;

В современных прикладных инженерных программных продуктах,

Например в Mathcad существуют специальные функции для вычисления норм матриц:

normi(A)

norm1(A)