Выводы
В результате моделирования были получены следующие результаты:
1). При ∆ t = tw - tи > 0 квадратичный критерий: Q = 0,0047567.
2). При ∆t = tw - tи < 0 квадратичный критерий: Q = 0,011937.
Таким образом, система регулирования по возмущению эффективна только в том случае, когда запаздывание в канале управления меньше, чем в канале возмущения. Контролируемые возмущения компенсируются практически в 100 % объеме.
При запаздывании в канале управления большем, чем в канале возмущения была сделана сдвижка, но она не дала необходимого влияния на выход объекта. Выходное воздействие по отклонению расходится с выходным воздействием по возмущению, и тем самым процесс получился неустойчивым.
1) Структура системы регулирования по отклонению 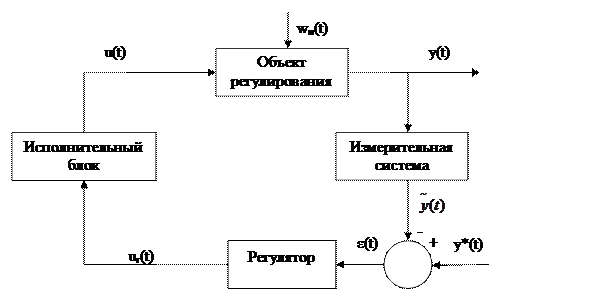
Рисунок 1 - Структура системы регулирования по отклонению
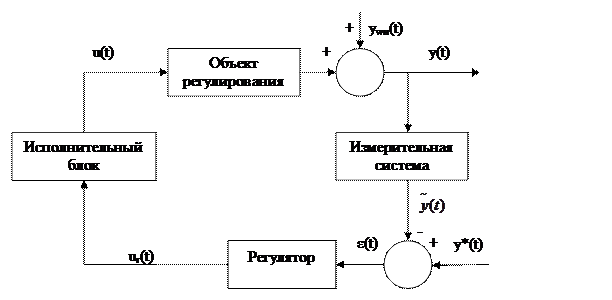
Рисунок 2 - Структура системы регулирования по отклонению с учётом приведённых возмущений
2) Математическая модель канала регулирования
В общем виде:
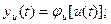
В конкретизированном:
y(i)=c1·y(i-1)+c2·u(i-l)
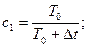
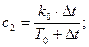
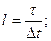
3) Модель приведённого к выходу возмущения 
X={Wk;ywн}
ГТФ - Генератор типовых функций
ГСЧ - генератор случайных чисел
Рисунок 3 - Модель приведённого к выходу возмущения
4) Закон регулирования
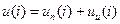 ;
;
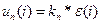 ;
;
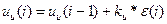 ;
;
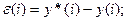
5) Среднеквадратический критерий точности регулирования
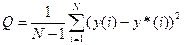
N - отрезок моделирования
6) Поисковая процедура
Рассмотрим функцию двух переменных. Ее линии постоянного уровня представлены на рис. 4, а минимум лежит в точке. (Напомним, что линией постоянного уровня называется кривая в двумерном сечении пространства параметров (в данном случае в плоскости (х1, х2), значение функции на которой - константа). Простейшим методом поиска является метод покоординатного спуска. Из точки А мы производим поиск минимума вдоль направления оси х1 и, таким образом, находим точку B, в которой касательная к линии постоянного уровня параллельна оси x1. Затем, производя поиск из точки B в направлении оси x2, получаем точку C, производя поиск параллельно оси x1, получаем точку D, и т.д. Таким образом, мы приходим к оптимальной точке. Любой из одномерных методов, описанных в предыдущей главе, может быть использован здесь для поиска вдоль оси. Очевидным образом эту идею можно применить для функций n переменных.
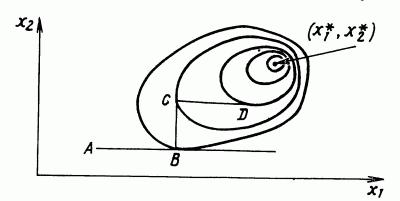
Рисунок 4 - Схема оптимизации методом покоординатного спуска
7) Начальные условия
y(0)=0,y(1)=1,y*(0)=0,y*(1)=1
Требуется:
1) Составить математическую модель системы регулирования по отклонению
1.1. В общем виде
1.2. В конкретизированном
2) Составить алгоритм моделирования системы регулирования по отклонению
3) Сделать программную реализацию системы регулирования по отклонению
4) Уточнить настройки закона регулирования путём математического моделирования и поисковой процедуры
5) Провести исследования; в процессе моделирования выяснить влияние величины τ/Такф на среднеквадратический критерий
6) Результаты представить в виде графика и таблицы
1.1. Математическая модель системы регулирования по отклонению в общем виде
1. y(t) = 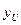 (t)+
(t)+ 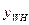 (t);
(t);
2. 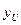 (t) =
(t) =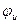 { u(t) };
{ u(t) };
3. u(t) = 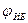 {
{ 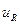 (t) };
(t) };
4. 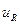 (t) =
(t) = 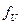 {
{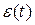 };
};
5. 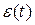 = y*(t) -
= y*(t) - 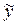 (t);
(t);
6. 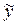 (t) =
(t) = 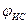 { y(t) };
{ y(t) };
7. 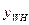 (t) =
(t) = 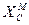 +
+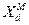 ;
;
8. 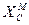 =
= 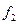 {
{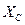 };
};
9. 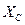 =
= 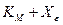 ;
;
10. 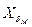 = f1 { ГСЧ};
= f1 { ГСЧ};
11. 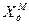 =
= 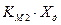 ;
;
12. 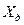 =
= 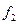 {ГТФ};
{ГТФ};
1.2. Математическая модель системы регулирования по отклонению в конкретизированном виде
1. 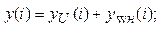
2. 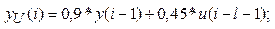
3. 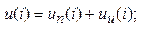
4. 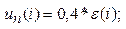
5. 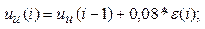
6. 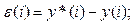
7. 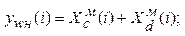
8. 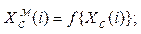
9. 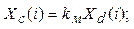
10. 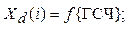
11. 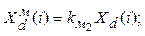
12. 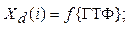
2. Алгоритм моделирования системы регулирования по отклонению
|
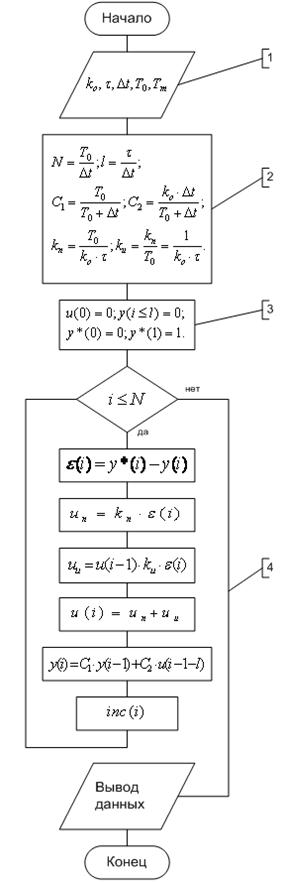
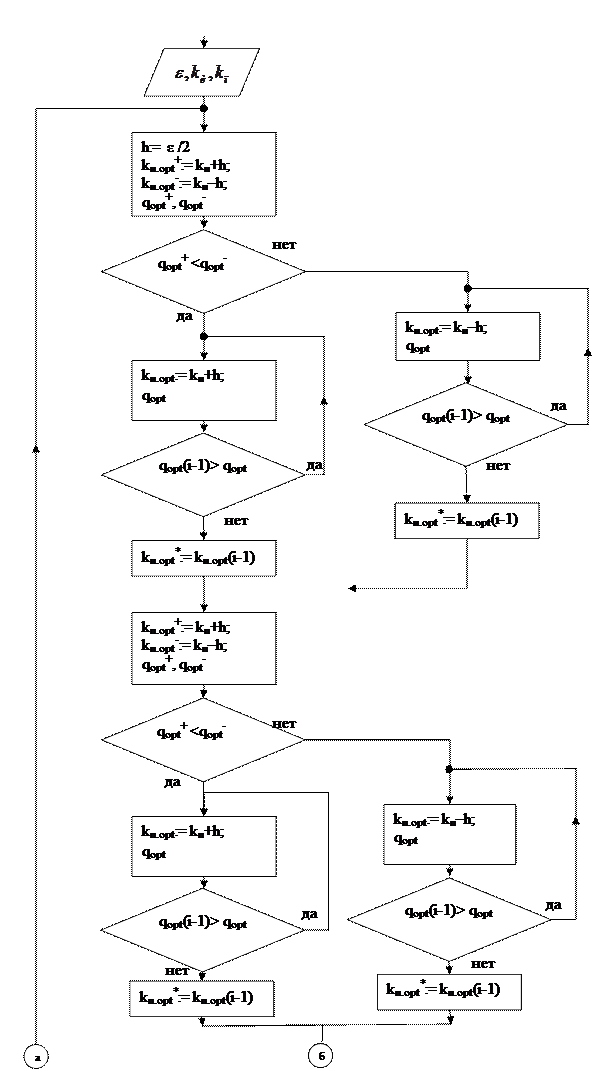
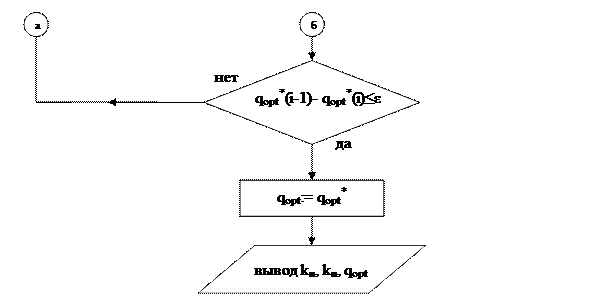
Ниже, на рисунке приведен алгоритм поиска оптимальных настроечных параметров


 2014-02-13
2014-02-13 539
539








