Вывод закона регулирования

В соответствии с принципом регулирования по возмущению управление должно содержать компоненту для компенсации возмущения.

Выходное воздействие системы можно представить в виде суммы двух составляющих: y(s) = y_u(s) + y_w(s), где y_u(s) = φ_u(s) ∙ u(s); y_w(s) = φ_w(s) ∙ w_к(s).

Для компенсации возмущения должно выполняться условие: y_u(s) = - y_w(s), т.е. φ_u(s) ∙ u(s) = - φ_w(s) ∙ w_к(s).

Таким образом, получаем следующее управление:

u(s) = - φ_w(s)/φ_u(s) ∙ w_к(s). (7)

Подставив в закон регулирования (7) математические модели получаем:

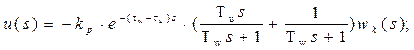(8)

где k_р = k_w/ k_и.

Данное регулирующее воздействие (8) можно представить в виде параллельного соединения двух звеньев: инерционного звена и реально-дифференциального: u(s) = u_и(s) + u_р.д(s). Тогда:

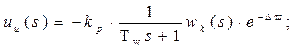(9)

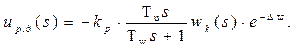(10)

Реально-дифференциальную составляющую можно представить в виде последовательного соединения звеньев: 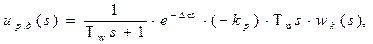или:

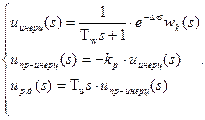(11)

Запишем систему уравнений для системы регулирования по возмущению при помощи аппарата передаточных функций:

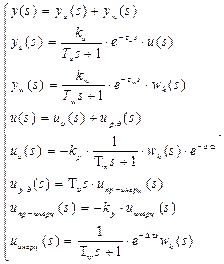(12)

Представим систему 12 с использованием непрерывных временных функций:

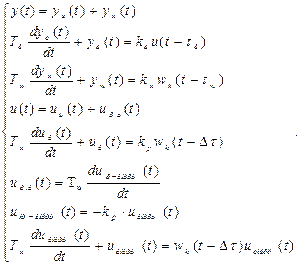(13)

Для записи системы (13) в виде дискретных временных функций воспользуемся методом левых конечных разностей. В результате получим:

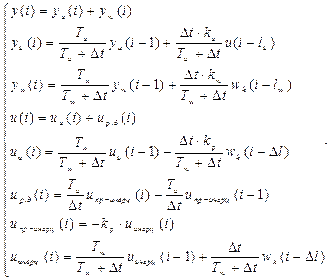(14)

где ∆t ‑ шаг дискретизации, ∆t =1;

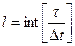‑ дискретное запаздывание.

В данной системе регулирования рассматривается два случая: когда запаздывание в канале управления меньше, чем в канале возмущения, т.е. t_w - t_и > 0, и, напротив, когда запаздывание в канале управления больше, чем в канале возмущения, т.е. t_w - t_и <0. В последнем случае в канале управления возникает упреждение, чего не может быть, поэтому необходимо сделать сдвижку, т.е. w_к(i-∆l)→ w_к(i). Тогда система (14) примет вид:

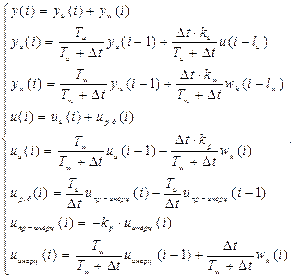(15)