Математическое моделирование системы регулирования по возмущению
Дано:
1) Блок-схема структуры системы регулирования по возмущению изображена на рисунке 1,
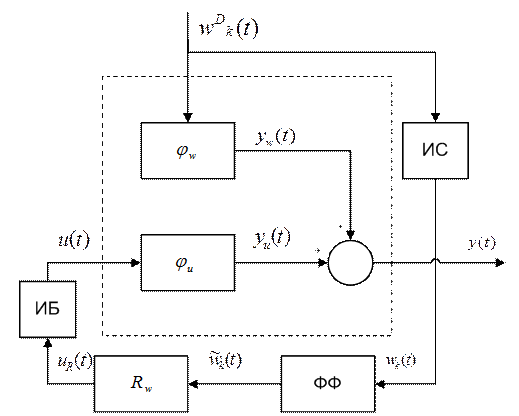
Рисунок 1 – Блок-схема структуры системы регулирования по возмущению
где 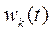 - контролируемые возмущения,
- контролируемые возмущения,
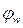 - математическая модель канала преобразования контролируемого возмущения,
- математическая модель канала преобразования контролируемого возмущения,
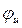 - математическая модель канала преобразования регулирующих воздействий,
- математическая модель канала преобразования регулирующих воздействий,
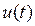 - регулирующие воздействия,
- регулирующие воздействия,
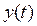 - выходное воздействие,
- выходное воздействие,
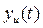 - выходное воздействие канала регулирования,
- выходное воздействие канала регулирования,
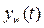 - выходное воздействия канала возмущений,
- выходное воздействия канала возмущений,
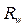 - регулятор.
- регулятор.
2) Математическая модель канала регулирования.
Модели каналов преобразования контролируемых возмущений и регулирующих воздействий φu(s) и φw(s) – инерционное звено первого порядка. Значения параметров:
1) kи = 1, Tи =70, tи = 7, kw = 1, Tw =70, tw = 12, ∆ t = tw - tи > 0;
2) kи = 1, Tи =70, tи = 12, kw = 1, Tw =70, tw = 7, ∆ t = tw - tи < 0.
3) Модели контролируемых возмущений, представленных в виде:
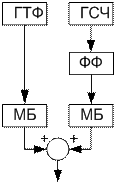
Рисунок 2 – Модель приведённых к выходу объекта неконтролируемых возмущений
где ГТФ – генератор типовых функций,
ГСЧ – генератор случайных чисел,
МБ – масштабирующий блок,
ФФ – формирующий фильтр.
4) Начальные условия: y(0) = 0, и(0) = 0, wк(0) = 0.
5) Поисковая процедура: метод покоординатного поиска.
6) Критерий точности – среднеквадратическое отклонение (СКО)
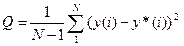
где 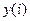 - значение выходной величины,
- значение выходной величины,
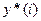 - заданное значение выходной величины.
- заданное значение выходной величины.
Требуется:
1) Построить математическую модель системы регулирования по отклонению:
1.1. В общем виде;
1.2. В конкретизированном виде.
2) Составить алгоритм моделирования системы регулирования по возмущению.
3) Программная реализация системы регулирования по возмущению.
4) Используя поисковую процедуру, найти такие параметры закона регулирования, при которых значение критерия точности регулирования минимально.
5) Провести анализ результатов.
 2014-02-13
2014-02-13 478
478








