Основные операции алгебры логики

Логические функции и способы их задания

Логические функции и их свойства

При построении дискретных устройств в настоящее время наибольшее распространение получили элементы, у которых входные и выходные сигналы принимают одно из двух возможных значений – высокий и низкий электрический потенциал, импульсы положительной и отрицательной полярности, наличие и отсутствие импульса тока, электрический ток большой и малой силы и т.д.

Поэтому для описания ДУ используются переменные, которые принимают также одно из двух возможных значений: 0 или 1, т.е. двоичные переменные.

Способ отождествления реальных сигналов с цифрами 0 и 1 может выбираться произвольно. Например, высокий электрический потенциал (наличие сигнала) можно сопоставить с цифрой 1, а низкий электрический потенциал (отсутствие сигнала) – с цифрой 0.

Возможности описывать условия функционирования ДУ дает алгебра логики (двоичная алгебра, булева алгебра).

Алгебра логики оперирует с логическими переменными и логическими функциями.

Логической, или двоичной, переменной называется величина, которая может принимать только два значения: 0 или 1. Логические переменные обозначаются буквами латинского алфавита. Логической функцией (функцией алгебры логики, переключательной функцией) называется функция, которая, как и ее аргументы (логические переменные), может принимать лишь одно из двух возможных значений: 0 или 1.

Логические функции выражают зависимость выходных переменных от входных.

В релейно-контактных устройствах значение 1 соответствует состоянию ИО и РО «включено», а значение 0 – состоянию «выключено».

Логические функции в зависимости от числа входных переменных делятся на функции одной переменной, двух переменных и многих переменных.

Различные комбинации значений входных переменных в логических функциях называются н а б о р а м и.

Например, две входных переменных, принимая значения 0 или 1, могут образовать всего четыре различных сочетания нулевых и единичных значений, т.е. 4 набора: 00, 01, 11, 10.

Для упорядочивания таких n -мерных двоичных наборов любой набор будем рассматривать как представление целого неотрицательного числа в двоичной системе счисления. При этом будем полагать, что в двоичном числе младший разряд расположен справа.

Например, набор 10011 может быть представлен десятичным числом

1 · 2⁴ + 0 · 2³ + 0 · 2² + 1 · 2¹ + 1 · 2⁰ = 19,

а набор 1110 – числом

1 · 2³ + 1 · 2² + 1 · 2¹ + 0 · 2⁰ = 14.

Для компактной записи наборов значений переменных логической функции целесообразно их представлять числами в десятичной или восьмеричной системах счисления.

Десятичное или восьмеричное число, которым представляется набор значений переменных логической функции, будем называть весовым состоянием (номером) или просто весом этого набора. С данным понятием мы уже встречались, когда рассматривали способы задания ДА.

Для однозначного задания двоичного набора значений переменных необходимо назвать его весовое состояние (номер) и размерность (базу), т.е. количество переменных логической функции и их взаимное расположение. Так, например, десятичному числу 25 соответствует набор 11001 при размерности n = 5 или набор 0011001 при размерности n = 7.

Так как каждая логическая переменная может принимать лишь два значения, то очевидно, что множество возможных комбинаций значений n переменных содержит 2 ⁿ двоичных наборов размерности n.

Определим максимальное количество различных логических функций от N переменных.

Для однозначного задания логической функции необходимо оговорить ее значение на каждом наборе переменных. В связи с тем, что на каждом наборе логическая функция может принимать значение 0 или 1 независимо от ее значений на остальных наборах переменных, а число наборов всегда равно 2 ⁿ, число различных логических функций определится выражением

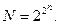
Например, для n = 1 число логических функций N = 4, для n = 2 N = 16, для n = 3 N = 256, для n = 4 N = 65 536, для n = 5 N = 4 294 966 296.

Как видно, с увеличением числа переменных количество логических функций очень быстро растет и уже для пяти переменных составляет огромную величину.

Наборы переменных, на которых логическая функция принимает значение 1, будем называть рабочими (единичными). Наборы, на которых функция принимает значение 0, будем называть запрещенными (нулевыми).

Функции, значения которых определены на всех 2 ⁿ наборах, называются полностью определенными логическими функциями. Нередко рассматриваются функции, значения которых определены только для части наборов. Такие функции будем называть не полностью определенными функциями.

Наборы переменных, на которых значение функций не определено, будем называть условными наборами. Значения функции на условных наборах могут выбираться произвольным образом.

Логические функции могут быть заданы:

- словесным описанием;

- таблицами соответствия (истинности);

- весовыми состояниями (номерами) рабочих, запрещенных и условных наборов (символическая форма);

- формулами (аналитическими выражениями).

При словесном описании логической функции должны быть указаны характерные ее свойства и перечислены совокупности рабочих, запрещенных и условных наборов.

Для задания логической функции таблицей соответствия строится специальная таблица, число строк которой равно числу различных наборов переменных (2 ⁿ), а число столбцов равно n + 1. Первые n столбцов обозначаются символами переменных, от которых зависит функция, а последний n + 1 столбец – символом функции. В каждую строку такой таблицы записывается набор значений переменных и соответствующее ему значение функции. Для полностью определенных функций в столбце значений стоят только 1 или 0. Для не полностью определенных функций в строках, соответствующих условным наборам, будем проставлять знак ~.

С целью уменьшения объема таблиц соответствия в связи с тем, что число строк 2 ⁿ очень быстро растет с увеличением числа переменных n, применяются с о к р а щ е н н ы е таблицы. Для полностью определенных функций сокращенные таблицы включают в себя только рабочие или только запрещенные наборы.

Примеры полной и сокращенных таблиц соответствия для полностью определенной функции от трех переменных представлены таблицами 2.1, 2.2, 2.3.

С целью сокращения таблицы соответствия не полностью определенной функции можно опустить либо единичные, либо нулевые, либо условные наборы. Например, логическую функцию, заданную таблицей соответствия (Таблица 2.4), можно представить одной из сокращенных таблиц соответствия (Таблицы 2.5-2.7).

	Таблица 2.1		Таблица 2.2
	x 3	x 2	x 1	f (x)		x 3	x 2	x 1	f (x)
						Таблица 2.3
						x 3	x 2	x 1	f (x)
	Таблица 2.4
	x 3	x 2	x 1	f (x)
						Таблица 2.5
				~		x 3	x 2	x 1	f (x)
				~
									~
				~					~
									~
	Таблица 2.6		Таблица 2.7
	x 3	x 2	x 1	f (x)		x 3	x 2	x 1	f (x)
				~
				~
				~

При задании функции сокращенной таблицей соответствия целесообразно выбирать вариант таблицы, содержащей минимальное количество строк.

Более компактным табличным способом задания логических функций является использование двухвходовых таблиц соответствия. При построении такой таблицы количество переменных, от которых зависит функция, разбивается на две примерно равные части (группы).

Для образования групп переменных определяются всевозможные наборы их значений. Столбцы и строки таблицы в произвольном порядке обозначаются наборами переменных первой и второй групп. Каждая клетка такой таблицы соответствует одному набору значений переменных, и в ней представлено значение функции на этом наборе. Общее количество клеток такой таблицы соответствует числу всевозможных наборов значений переменных.

Примером двухвходовой таблицы соответствия для функции от четырех переменных является таблица 2.8.

			Таблица 2.8
			x 4 x 3	x 2 x 1
							~
					~
					~	~

Удобно для задания логических функций использовать весовые состояния рабочих, запрещенных и условных наборов в десятичной или восьмеричной системах счисления. Для этого должны быть перечислены номера (весовые состояния) всех рабочих, запрещенных и условных наборов. Такой способ задания называют иногда символической формой.

Очень важно, чтобы для однозначности задания логической функции при записи ее были перечислены переменные, от которых зависит функция, обязательно в том порядке, в каком их значения расположены в двоичных наборах, т.е. должна быть указана база.

Например, если приведен такой порядок логических переменных: x ₄, x ₃, x ₂, x ₁ и среди номеров рабочих наборов имеется десятичное число 13, то это означает, что при значениях переменных x ₁ = 1, x ₂ = 0, x ₃ = 1, x ₄ = 1 (двоичный набор 1101) значение логической функции равно 1.

Заметим, что весовое состояние набора есть десятичное или восьмеричное представление двоичного числа, соответствующего значению переменных набора.

Выбор базы, т.е. определенного положения переменных в наборе, можно понимать как присвоение каждой переменной (каждому разряду двоичного набора) определенных весов двоичного счисления, причем самый малый вес 2⁰ присваивается правому разряду, а затем справа налево веса увеличиваются. Так, в нашем примере переменная x ₁ имеет вес 2⁰, x ₂ – 2¹, x ₃ – 2², x ₄ – 2³. Тогда весовое состояние набора представляет собой сумму весов тех переменных (разрядов) набора, которые имеют значение, равное 1.

При задании логической функции весовыми состояниями рабочих и запрещенных наборов (символической формой) условимся, как и при задании ДА, рабочие ВС указывать через запятую, запрещенные – в квадратных скобках, условные – в круглых скобках. Базу будем указывать в обозначении функции, систему счисления при необходимости – в виде нижних индексов у функции.

Например, логическая функция, описанная таблицей соответствия (Таблица 2.8), может быть задана в символической форме:

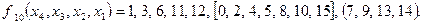
Функция, описанная таблицей 2.4, также задана в символической форме:

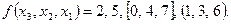
Очевидно, что при задании функции символической формой достаточно указывать рабочие и запрещенные ВС, или рабочие и условные, или запрещенные и условные.

Недостающие наборы определяются в каждом случае как дополнительные до полного числа 2 ⁿ.

Так, последняя функция может быть задана в виде

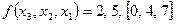
или

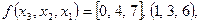
или

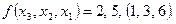
В случае полностью определенных функций достаточно указать только рабочие или только запрещенные ВС. Обычно при употреблении десятичной системы счисления нижние индексы у функций не ставятся, в остальных случаях необходимо указать систему счисления нижним индексом у функции, например:

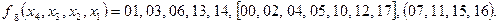
Произвольная логическая функция может быть задана в виде аналитического выражения (формулы), которое представляет собой совокупность переменных, объединяемых определенными операциями (конъюнкция, дизъюнкция, инверсия и др.).

Аналитические формы представления (задания) логических функций будут рассмотрены позднее.

Математическим аппаратом теории ДУ является алгебра логики. Любая алгебра вводится основными операциями и законами (аксиомами).

Основными операциями алгебры логики являются:

- логическое сложение (дизъюнкция);

- логическое умножение (конъюнкция);

- логическое отрицание (инверсия).

Логическое сложение (дизъюнкция) обозначается символом 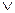(«+», ИЛИ). Логическая сумма обозначает сложное суждение, состоящее из простых суждений, объединяемых союзом ИЛИ. Логическая сумма равна 1, если хотя бы одно из слагаемых равно 1.

Логическое умножение (конъюнкция) обозначается символом 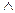(«·», &, И). Логическое произведение обозначает сложное суждение, состоящее из простых суждений, объединяемых союзом И. Логическое произведение равно 1, если все сомножители равны 1.

Логическое отрицание (инверсия) обозначается символом «–». Логическое отрицание представляет собой суждение, противоположное данному, и читается с частицей НЕ: 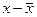(НЕ x).