Рабочих и запрещенных обобщенных кодов

Минимизация логических функций методом поразрядного сравнения

Часто при синтезе сложных дискретных устройств, особенно микропрограммных автоматов (МПА), условия их работы, т.е. логические функции (ЛФ), описывающие возбуждение элементов памяти и появление сигналов на выходе, получаются сразу в обобщенных кодах (ОК) – рабочих и запрещенных. Для их минимизации методом поразрядного сравнения рабочих и запрещенных весовых состояний ОК можно перевести в рабочие и запрещенные весовые состояния в восьмеричной системе счисления, но этот путь долгий и сложный.

Разработан (Викентьевым Л. Ф.) метод минимизации ЛФ, не полностью определенных, заданных рабочими и запрещенными ОК.

Рассмотрим его.

Рабочий ОК – это ОК, описывающий такие наборы переменных, на которых ЛФ равна 1, т.е. покрывающий попарно соседние рабочие весовые состояния (ВС).

Запрещенный ОК – это ОК, описывающий такие наборы переменных, на которых ЛФ равна 0, т.е. покрывающий попарно соседние запрещенные ВС.

Разряды обобщенного кода, занятые символами 1 и 0, называются значащими разрядами ОК. Количество тире в ОК называется рангом ОК.

Сущность метода минимизации не полностью определенных ЛФ, заданных рабочими и запрещенными ОК, заключается в том, что поочередно рассматриваются рабочие ОК (сравниваются с запрещенными ОК), в которых стараются как можно больше значащих разрядов заменить символами «–» (тире), стремясь получить ОК максимального ранга, включающий в себя как можно больше рабочих ОК и не включающий ни одного запрещенного.

Методика минимизации заключается в следующем. Каждый рабочий ОК сравнивается со всеми запрещенными ОК, и в нем оставляют лишь те минимально необходимые значащие разряды, которые отличают его от всех запрещенных ОК.

Получают результирующий рабочий ОК, содержащий минимальное число значащих разрядов.

Если в ходе сравнения получаются одинаковые результирующие ОК (а к этому всегда надо стремиться), то по закону повторения оставляют только один из них.

Совокупность полученных результирующих ОК образует приведенную систему простых импликант, а дизъюнкция соответствующих им членов ДНФ является одной из частных МДНФ (одной из тупиковых ДНФ).

Пример 3.14 Получена таблица соответствия для функции Z ₁ при базе y ₂ y ₁ x ₃ x ₂ x ₁.

Каждая строка таблицы представляет собой ОК, первые четыре строки – рабочие ОК, последние три строки – запрещенные ОК.

По очереди сравниваем каждый рабочий ОК с каждым запрещенным ОК и минимально необходимые для их различия значащие разряды обводим «рамкой». Запишем результирующие ОК, объединим повторяющиеся, перейдем к импликантам при заданной базе (Таблица 3.6).

Получим частную МДНФ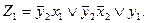

Поскольку двоичное число является частным случаем обобщенного кода – обобщенный код нулевого ранга, то, очевидно, этот метод можно применять для минимизации ЛФ, зависящих от любого числа переменных и заданных в СДНФ или символической формой. При этом следует рабочие и запрещенные весовые состояния (члены СДНФ) записать в виде ОК (двоичных чисел) и поступать, как указано выше.