Анализ дискретных устройств

Общие выводы

Таблица 3.6

y 2	y 1	x 3	x 2	x 1	Z 1	Результирующий ОК	Импликанта
		–	–			0 – – – 1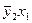
		–				0 – 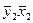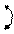– 0 –
0		–	–			– 1 – – –	y 1
		–	–			– 1 – – –
		–
			–	–
			–	–

Поясним это на примерах, рассмотренных ранее.

Пример 3.15 Минимизировать функцию 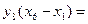37, 22, 31, [00, 16, 10].

Перейдем от ВС к ОК и выполним минимизацию.

	→	011 111	→	– 1 – – – –	– 1 – – – –
	→	010 010	→	– 1 – – – –	→	x 5
	→	011 001	→	– 1 – – – –
	→	000 000
	→	001 110
	→	001 000

Получили ответ такой же, как и ранее y = x ₅, трудовые затраты – меньше.

Заметим, что если ВС много, то желательно соседние ВС объединять в ОК.

Пример 3.16 Минимизировать ЛФ 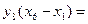73, 66, 43, 52, 56, 67, [00, 03, 15, 22, 23, 37, 40]

111 011		111 011	1 – – – 1 –	→	x 6 x 2
110 110		110 11–
100 011		100 011
101 010		101 –10
101 110
110 111
000 000		–00 000
000 011		0–0 011
001 101		001 101
010 010
010 011
011 111		011 111
100 000

Получили тот же результат y = x ₆ x ₂, трудовые затраты – больше, большая вероятность ошибки.

Пример 3.17 Минимизировать ЛФ 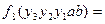21, 22, 27, [06, 20, 24, 26].

21	→	10 001	→	10 001		– – – – 1	→	b
	→	10 010	→	10 0|10		– – 01 –	→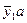
	→	10 111	→	10 111
	→	00 110		–0 110
	→	10 000		10 –00
	→	10 100
	→	10 110

Получили ответ .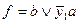

Различные методы минимизации следует применять:

1. Для полностью определенных ЛФ – прямой метод склеивания конституент (метод Квайна – Мак-Класски).

2. Для не полностью определенных ЛФ до четырех переменных – метод решетки соседних чисел или карт Карно.

3. Для не полностью определенных ЛФ более четырех переменных – метод поразрядного сравнения рабочих и запрещенных весовых состояний с использованием восьмеричной системы счисления.

4. Для не полностью определенных ЛФ более четырех переменных, когда условия работы получены в обобщенных кодах (или их легко получить, или мало рабочих и запрещенных наборов) – метод сравнения рабочих и запрещенных обобщенных кодов.