Если применить соотношение неопределенностей между энергией и временем к спонтанному распаду в системах, находящихся в квазистационарных состояниях, т.е. в состояниях, которые существуют конечное время, то D t – можно рассматривать как среднее время жизни t этого состояния. Тогда D Е – представляет собой неопределенность энергии этого состояния. В этом случае можно ввести еще одну, часто используемую величину – ширину уровня 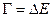 . Тогда выражение
. Тогда выражение 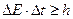 приобретает вид
приобретает вид 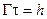 .
.
В данной форме соотношение неопределенностей играет большую роль в атомной и ядерной физике. Пусть при распаде испускается квант с энергией 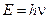 . Неопределенность в значении энергии приводит к неопределенности (разбросу) энергии фотона и, как следствие, к спектральному распределению интенсивности
. Неопределенность в значении энергии приводит к неопределенности (разбросу) энергии фотона и, как следствие, к спектральному распределению интенсивности 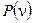 электромагнитных волн. Тогда, если заменить символ ширины энергетического уровня G символом спектрального распределения g, то равенство
электромагнитных волн. Тогда, если заменить символ ширины энергетического уровня G символом спектрального распределения g, то равенство 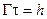 переходит в равенство
переходит в равенство 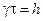 .
.
Профиль спектрального распределения (спектральной линии) описывается распределением Лоренца: 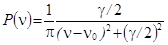 (см. рис, где показан вид функции Р (n) при g =1 (кривая 1) и при g =3 (кривая 2) и n0 = 0).
(см. рис, где показан вид функции Р (n) при g =1 (кривая 1) и при g =3 (кривая 2) и n0 = 0).
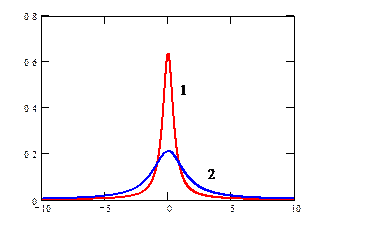 Смысл параметра g - это ширина линии на половине ее высоты; она называется естественной шириной линии. При переходах между двумя состояниями с энергетической шириной Г1 и Г2 спектральная ширина линии равна
Смысл параметра g - это ширина линии на половине ее высоты; она называется естественной шириной линии. При переходах между двумя состояниями с энергетической шириной Г1 и Г2 спектральная ширина линии равна 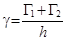 .
.
Таким образом, уравнение 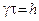 описывает фундаментальное свойство волн: оно связывает между собой конечную продолжительность t ограниченного волнового пакета с его спектральной шириной g. В свою очередь, это означает, что ограниченные во времени волновые пакеты не могут быть монохроматическими в принципе.
описывает фундаментальное свойство волн: оно связывает между собой конечную продолжительность t ограниченного волнового пакета с его спектральной шириной g. В свою очередь, это означает, что ограниченные во времени волновые пакеты не могут быть монохроматическими в принципе.
 2014-02-13
2014-02-13 2466
2466
