Спектральное разложение стационарного случайного процесса

Стационарный случайный процесс может быть представлен каноническим разложением вида:

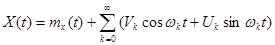, (6.41)

где V_k и U_k –некоррелированные и центрированные случайные величины с дисперсиями D [ V_k ] = D [ U_k ] = D_k; w – неслучайная величина (частота).

В этом случае каноническое разложение корреляционной функции определяется выражением

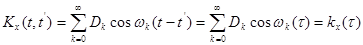, (6.42)

Каноническое разложение (6.41) называется спектральным разложением стационарного случайного процесса. Спектральное разложение (6.41) может быть также представлено в виде

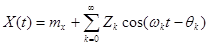, (6.43)

где q_k – фаза гармонического колебания элементарного стационарного случайного процесса, являющаяся случайной величиной равномерно распределенной в интервале (0, 2 p); Z_k – амплитуда гармонического колебания элементарного стационарного случайного процесса – тоже случайная величина.

Случайные величины q_k и Z_k зависимы. Для них имеют место соотношения:

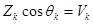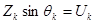, . (6.44)

Таким образом, стационарный случайный процесс может быть представлен в виде суммы гармонических колебаний со случайными амплитудами Z_k и случайными фазами q_k на различных неслучайных частотах w_k.

Так как корреляционная функция стационарного случайного процесса X (t) является четной функцией своего аргумента, т. е. k_x (t) = k_x (–t), то ее на интервале (– T, T) можно разложить в ряд Фурье по четным (косинусам) гармоникам

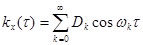, (6.45)

где w_k и D_k определяются выражениями:

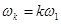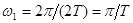, , (6.46)

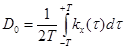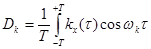, . (6.47)

Подставляя в выражение (6.45) t = 0, получим каноническое разложение для дисперсии стационарного случайного процесса:

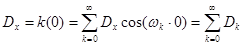. (6.48)

Таким образом, дисперсия стационарного случайного процесса, представленная своим каноническим разложением (6.41), равна сумме дисперсий всех гармоник его спектрального разложения.

Используя формулы (6.45 – 6.47) при k = 1, 2, 3, …, можно построить график изменения дисперсий D_k по частотам w_k (рис.6.7). Зависимость D_k = f (w_k)в этом случае называется дискретным спектром дисперсий или просто – дискретным спектром стационарного случайного процесса.

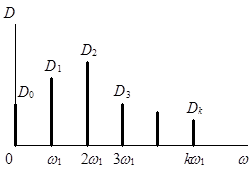
Рис.6.7. Дискретный спектр стационарного случайного процесса.

Если увеличивать интервал разложения (– T, T), то интервал между частотами будет сокращаться так как

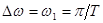. (6.49)

В пределе, при 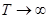(т. е. при 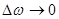) мы перейдем к непрерывному спектру.

В качестве характеристики распределения дисперсии по частотам непрерывного спектра используется спектральная плотность – S_x (w), которую можно рассматривать, как предел отношения дисперсии приходящейся на каждую частоту к D w:

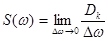. (6.50)

В этом случае выражение (6.45) примет вид:

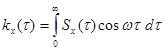. (6.51)

Таким образом, корреляционная функция и спектральная плотность стационарного случайного процесса связаны косинус-преобразованием Фурье. Следовательно, спектральная плотность стационарного случайного процесса может быть выражена через корреляционную функцию по формуле

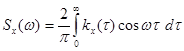. (6.52)

Спектральная плотность обладает следующими свойствами.

1. Она является неотрицательной функцией частоты:

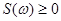. (6.53)

2. Интеграл от спектральной плотности в пределах от 0 до ∞ равен дисперсии стационарного случайного процесса:

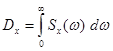. (6.54)

По аналогии с нормированной корреляционной функцией вводится нормированная спектральная плотность:

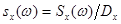. (6.55)

Нормированная корреляционная функция и нормированная спектральная плотность также связаны между собой преобразованием Фурье:

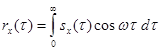, (6.56)

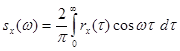. (6.57)

Интеграл от нормированной спектральной плотности в пределах от 0 до ∞ равен единице:

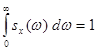. (6.58)

Таким образом, если на графике нормированной спектральной плотности (рис.6.8) рассматривать полосу частот от w ₁ до w ₂, то площадь подграфика, заключенная в интервале от w ₁ до w ₂, будет равна доле дисперсии случайного процесса, приходящейся на эти частоты. При этом общая площадь подграфика будет равна единице.

Рис.6.8. Нормированная спектральная плотность стационарного случайного процесса; заштрихованная площадь численно равна доле дисперсии, приходящейся па полосу частот от w ₁ до w ₂.

Следует отметить, что в специальной литературе встречаются различные определения спектральной плотности, отличающиеся постоянным множителем (табл.6.1). Достоинством первого определения является то, что для действительных случайных процессов при его использовании выполняются условия (6.54) и (6.58).

Таблица 6.1

Различные определения спектральной плотности

№	Спектральная плотность	Корреляционная функция

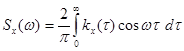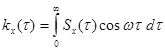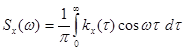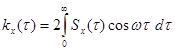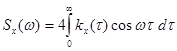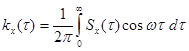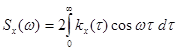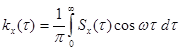При аналитических расчетах нередко используется спектральная плотность в комплексной форме 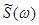. В этом случае рассматриваются как положительные, так и отрицательные частоты, а 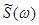и S (w) связаны соотношением:

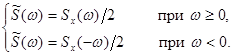(6.59)

Спектральная плотность в комплексной форме обладает следующими свойствами:

1. 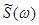является неотрицательной функцией частоты, то есть:

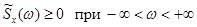. (6.60)

2. Интеграл от 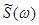в бесконечных пределах равен дисперсии случайного процесса:

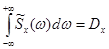. (6.61)

3. 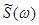– четная функция аргумента w:

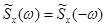. (6.62)

Пара преобразований Фурье для корреляционной функции и спектральной плотности в комплексной форме имеет вид:

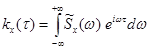, (6.63)

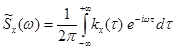. (6.64)

Следует отметить, что если спектральную плотность для действительных случайных процессов рассматривать как часть спектральной плотности 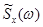, лежащую в области положительных частот, то мы получим определение S (w), приведенное в строке 2 таблицы 6.1. Однако в этом случае интеграл от нормированной спектральной плотности будет равен 0.5, а не единице, что с формальной точки зрения не очень хорошо.