Соотношения неопределенности Гейзенберга

Естественные пределы измерений

При измерении макроскопических величин максимальная точность ограничена статистическими флуктуациями возле среднего значения. Если эти флуктуации нельзя уменьшить при фиксированных внешних условиях, то их обычно называют шумами. Причины появления шумов можно разделить на три группы:

- корпускулярно-волновой дуализм микрочастиц материи (фотонов, электронов), который выражается соотношениями неопределенностей квантовой механики (соотношениями неопределенностей Гейзенберга);

- тепловые колебания микрочастиц вещества и электричества (электроны, атомы, ионы) при ненулевой температуре (равновесный шум);

- корпускулярная природа вещества и электричества, приводящая к нестабильности электрического тока (избыточный или неравновесный шум).

Существование принципа неопределенности обусловлено корпускулярно-волновой природой (дуализмом) материального мира, в котором состояние микросистем описывается волновой функцией, квадрат модуля которой представляет собой плотность вероятности реализации данного состояния. Это означает, что каждое наперед заданное значение физической величины будет появляться с той или иной вероятностью, зависящей от способа измерения.

Таким образом, физические параметры любых систем имеют статистическую природу и, в частности, означает, что повторение измерений в одних и тех же условиях даст разные результаты.

Вид волновой функции, в принципе, можно найти, решив соответствующее волновое уравнение (например, уравнение Шредингера или уравнение Дирака). Однако это уравнение, как правило, является нелинейным, и решить его чрезвычайно сложно. До настоящего времени оно решено лишь для нескольких простейших случаев.

Принцип неопределенности, сформулированный Гейзенбергом в 1927 г., является математическим выражением корпускулярно-волнового дуализма. Он позволяет оценить фундаментальные ограничения на предельную точность, с которой можно определить динамические переменные (физические параметры) системы, не решая волнового уравнения. Существование принципа неопределенности можно считать законом природы, более общим, чем волновое уравнение.

Принцип неопределенности утверждает, что отдельная величина может быть определена, в принципе, с любой степенью точности, однако две сопряженные физические величины (сопряженные пары физических величин определены в квантовой механике), нельзя одновременно определить сколь угодно точно. Это объясняют тем, что сам процесс измерения не возможен без обмена энергий с объектом измерения, и этот обмен возмущает этот объект.

Мерой разброса результатов измерений является среднее квадратическое отклонение s или дисперсия 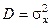статистически распределенной физической величины. В таком контексте эту величину называют “неопределенностью D”. Например, неопределенность (погрешность измерения) координаты .

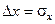Соотношение неопределенностей для координаты и сопряженной ей переменной - проекции импульса р _х – имеет вид 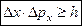. Отсюда следует, что одновременно точно измерить координату частицы и соответствующую проекцию импульса невозможно: чем меньше погрешность D х измерения координаты, тем больше погрешность D р _х измерения импульса ().

Поскольку постоянная Планка h»6,623×10^-34 Дж×с чрезвычайно мала, то соотношение неопределенностей при макроскопических измерениях лишено практического смысла. Неопределенности координаты и импульса, которые следуют из него, лежат далеко за пределами достижимой точности экспериментов.

Аналогично формулируется соотношение неопределенностей для другой пары сопряженных величин – энергии и времени: 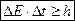. Это соотношение рассматривают или как связь погрешности измерения энергии атомной системы с погрешностью измерения времени D t, в течение которого измеряется энергия, или как связь изменения энергии атомной системы со временем, за которое это изменение произошло.