Типы рекурсивных частотных фильтров

Рекурсивные цифровые фильтры, как и нерекурсивные, не могут обеспечить реализацию идеальной частотной характеристики со скачкообразными переходами от полосы пропускания к полосе подавления. Поэтому на этапе решения аппроксимационной задачи необходимо определить передаточную функцию H(w) фильтра, которая обеспечивает воспроизведение необходимой амплитудно-частотной характеристики (АЧХ) с требуемой точностью. Требования к фазочастотной характеристике (ФЧХ) частотных фильтров, как правило, не задаются, т. к. это приводит к резкому усложнению решения задачи. Специальные требования к форме ФЧХ обычно реализуются после расчета фильтров с заданной АЧХ путем контроля полученной при этом ФЧХ и разработкой, при необходимости, дополнительных корректоров ФЧХ.

Синтез рекурсивных фильтров, как и НЦФ, выполняется на базе фильтров низких частот (ФНЧ). Другие типы фильтров (ФВЧ - высоких частот, ПФ - полосовые, РФ - режекторные) образуются на основе ФНЧ путем частотного преобразования.

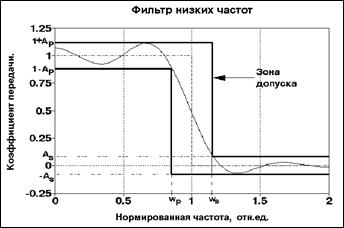
Рис. 6.4.1. Частотная характеристика ФНЧ.

Аппроксимационная задача низкочастотного фильтра.В качестве основных исходных данных для решения аппроксимационных задач принимаются граничные частоты w_p - полосы пропускания, и w_s – начала полосы подавления сигнала. Как правило, задаются также допуски А_p - на максимальное значение неравномерности в полосе пропускания, и А_s – на максимальное отклонение АЧХ от нуля в полосе подавления (уровень шума фильтра). Разность между граничными частотами w_p и w_s будет определять ширину переходной зоны. Типичный пример задания формы АЧХ приведен на рис. 6.4.1. В допустимой зоне передаточной функции условно показана возможная форма АЧХ, удовлетворяющая заданным условиям.

Кроме основных частотных параметров могут задаваться и требования к форме АЧХ (монотонность в полосе пропускания или подавления, характер пульсаций и т.п.), которые определяют выбор функции аппроксимации.

Передаточная функция. При решении аппроксимационной задачи амплитудно-частотная характеристика фильтра обычно задается в действительной аналитической форме - виде квадрата передаточной функции, нормированной по амплитуде и граничной частоте передачи:

|H(W)|² = H(W)·H*(W) = 1/(1+A_n(W)), (6.4.1)

где А_n(W) - многочлен n-го порядка, W - нормированная частота (например, W = w/w_p). Вид многочлена А_n(W) выбирается таким образом, чтобы выполнялось условие: А_n(W) << 1 при 0<W<1, что обеспечивает |H(W)|² ® 1, и A_n(W) >> 1 при W>1, соответственно |H(W)|² ® 0. Крутизна переходных зон фильтра устанавливается величиной порядка фильтра (чем больше значение n, тем больше крутизна переходных зон).

По знаменателю правой части выражения (6.4.1) достаточно просто могут быть определены комплексные полюса передаточной функции в p-области преобразования Лапласа и соответствующим комбинированием и объединением комплексно-сопряженных полюсов получены передаточные функции в виде биквадратных блоков при четном порядке, и с одним линейным блоком при нечетном порядке:

H(p) = G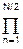В_n(p), n-четное, (6.4.2)

H(p) = 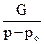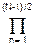В_n(р), n-нечетное, (6.4.3)

где В_n(р) выражается в форме:

В_n(p) = 1/[(p-p_n)(p-p_n*)] = 1/(p²-2 a_np+b_n). (6.4.4)

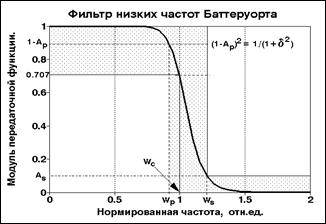
Рис. 6.4.2. АЧХ фильтра Баттеруорта.

Виды фильтров. В настоящее время существует достаточно большое количество видов рекурсивных частотных фильтров и их различных модификаций. Наиболее известный из них - фильтр Баттеруорта (рис.6.4.2). Он имеет монотонную гладкую АЧХ во всем частотном диапазоне. При том же порядке многочленов фильтров (равном количестве полюсов) большую крутизну обеспечивают фильтры Чебышева – прямой и инверсный, однако при этом в полосе пропускания (для инверсного – в полосе подавления) у фильтров Чебышева появляются равноволновые пульсации (с одинаковой амплитудой пульсаций). Еще более крутые срезы характеристик (при равноволновых пульсациях как в полосах пропускания, так и в полосе подавления) реализуются с использованием эллиптических функций.