Критическое состояние вещества

Как было отмечено выше, в критическом состоянии нет различия между жидкостью и газом, нет границы раздела между этими фазами. На диаграмме Ван-дер-Ваальса критическое состояние вещества изображается точкой перегиба К. Критическое состояние можно описать при помощи критических параметров состояния: критической температуры Т_к, критического объёма V_к и критического давления Р_к. Критические параметры можно выразить через поправки на давление и объём. Поскольку критическая точка – точка перегиба изотермы Ван-дер-Ваальса, то в этой точке первая и вторая производные от давления по объёму должны быть равны нулю. Поскольку состояние реального газа описывается уравнением Ван-дер-Ваальса, то первая производная определяется формулой:

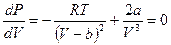(6.5)

Вторая производная: .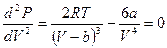

Приведём к общему знаменателю обе формулы и их числители приравняем нулю, получим: .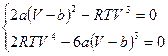

Преобразуем эту систему к уравнению: 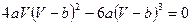. Поделим обе части этого уравнения на 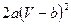и получим:

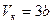(6.6)

На практике обычно . Для выражения критической температуры через поправки на объём и давление, воспользуемся формулой (6.5)и получим 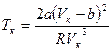. Подставим в эту формулу вместо критического объёма правую часть равенства (6.6) и получим:

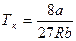(6.7)

Следует обратить внимание на то, что критическая температура вещества не равна температуре кипения. Так температура кипения воды 373,15 К, а критическая температура 647,25 К. Ниже приведены критические температуры некоторых веществ.

Вещество	Критическая температура, К
Вода (водяной пар)	647,25
Кислород	154,3
Азот

Критическое давление найдём, подставив в уравнение 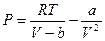критический объём и критическую температуру, выраженные через поправки Ван-дер-Ваальса, получим:

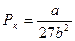(6.8)

Следует отметить, что для одного моля идеального газа справедливо равенство 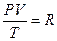. Поскольку в критическом состоянии газ нельзя считать идеальным, то приведённое выше равенство не выполняется, а справедливо следующее равенство:

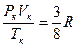(6.9)

При критических параметрах парообразное и жидкое состояния неразличимы. Однако, если при критической температуре , вещество находится в газообразном состоянии, а при 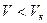- в жидком. Критические параметры обычно определяют экспериментально и по ним рассчитывают поправки Ван-дер-Ваальса. Для многих веществ трудно экспериментально измерить критические параметры. 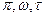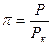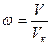В этом случае критические параметры рассчитывают, используя экспериментально полученные критические параметры другого вещества, и уравнение Ван-дер-Ваальса в приведённых или относительных параметрах: , где , и 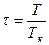. Уравнение Ван-дер-Ваальса в приведённых или относительных параметрах имеет вид для одного моля:

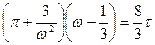(6.10)

Таким образом, изучение поведения уравнения (6.10) позволяет предсказать поведение любого реального газа.

6.5 Внутренняя энергия и теплоёмкость реального газа

Внутренняя энергия и теплоёмкость реального газа определяется кинетической энергией теплового движения его молекул и потенциальной энергией их взаимодействия:

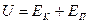(6.11)

Для одного моля газа 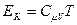. Потенциальную энергию определим, если учтём, что элементарная работа сил молекулярного взаимодействия при постоянной температуре определяется по формуле: 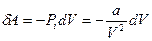. Эта работа связана с изменением потенциальной энергии известным равенством: . Тогда 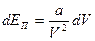. Интегрируя это выражение, получим: 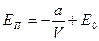. Примем Е_П=0 при 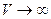, следовательно, Е₀ = 0. Тогда потенциальная энергия одного моля реального газа будет определяться формулой:

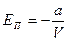(6.12)

С учётом этого внутренняя энергия одного моля реального газа равна:

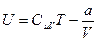(6.13)

Таким образом, внутренняя энергия реального газа зависит не только от температуры, но и от объёма. Температура реального газа может меняться даже в том случае, когда его внутренняя энергия остаётся постоянной.

Определим теплоёмкость реального газа. Согласно определению, теплоёмкость газа определяется формулой:

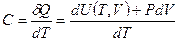(6.14)

Для реального газа 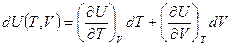. С учётом этого, теплоёмкость реального газа будет определяться формулой:

(6.15)

Рассмотрим частные случаи. Определим молярную теплоёмкость при постоянном объёме для реального газа. Так как изменение объёма равно нулю, то второе слагаемое в уравнении (6.15) тоже будет равно нулю, а теплоёмкость будет такой же, как и у идеального газа:

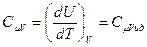(6.16)

Молярная теплоёмкость при постоянном давлении для реального газа будет отличаться от таковой для идеального газа вследствие учёта взаимодействия между молекулами и будет определяться по формуле:

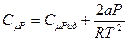(6.17)

Разность между молярными теплоёмкостями реального газа уже не будет равна универсальной газовой постоянной, а будет определяться выражением:

(6.18)

Показатель адиабаты тоже будет отличаться от показателя для идеального газа:

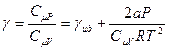(6.19)

В отличие от идеальных газов 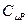и g для реального газа Ван-дер-Ваальса зависит от температуры и давления, и заметно отличаются от значений для идеального газа при высоких давлениях и низких температурах, поскольку второе слагаемое в уравнении (6.19) при этом растёт.