2014-02-13
615
Лекция 10
Пусть рассматривается линейная модель вида
у(х,b)=b0 + b1 x1 +...+ bk xk. (6.2)
Для оценки коэффициентов и анализа полученных результатов используется ПФП вида 2k или ДФП вида 2k-m. В каждой точке плана проводится один эксперимент. Так как ошибки наблюдений в общем случае складываются из случайных и систематических, то для компенсации влияния систематических ошибок наблюдения рандомизируются во времени, т.е. проводятся в случайной последовательности. Выбор очередной точки наблюдения производится случайным образом равновероятно из оставшихся.
Ошибки наблюдений считаются везде независимыми нормально распределенными случайными величинами с 
; 
. Тогда матрица весов наблюдений будет единичной: W = Е. Для оценки ошибки наблюдений в одной из точек плана (как правило, в центральной точке) проводится п0 экспериментов. Матрица F имеет вид
В соответствии с МНК нормальные уравнения имеют вид 
, отсюда уравнения для коэффициентов регрессии будут: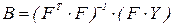 
.
Информационная матрица 
диагональная, невырожденная и равна: М = N Ek+1. Дисперсионная матрица также диагональна и равна: 
. Следовательно, оценки коэффициентов регрессии независимы и равны:
i=1,...,К.
В случае ДФП коэффициенты b1 включают в себя эффекты взаимодействия в соответствии с генерирующими соотношениями, используемыми при построении плана. Дисперсия оценок коэффициентов регрессии равна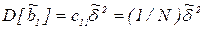 
i = 0,...,k. Как видим для всех Di она одинакова.
Оценка дисперсии воспроизводимости ищется по п0 наблюдениям в центре плана х0:
, где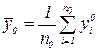 
Оценка дисперсии адекватности:
, где 
Для проверки адекватности модели вычисляется статистика: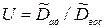 
, подчиненная F-распределению с числом степеней свободы rад = N-(k+l) (числитель), rвос = п0-1 (знаменатель). Если и<икр, то модель адекватна.
Для проверки значимости коэффициентов DI используется статистика: 
, подчиненная t-распределению с rb=n0-l.
Если lU1l < UKp, то коэффициент b1 - незначим.
Для проверки значимости влияния квадратичных факторов, как и ранее, используется статистика U (6.1), подчиненная t-распределению с числом степеней свободы г=n0-1. Если U < Uкр, то влияние квадратов x12 незначимо и им можно пренебречь.
Дисперсия оценки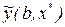 
, вычисленной по уравнению регрессии, будет:
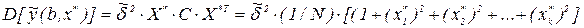
где х* задается в стандартизованном виде: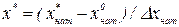 
. Как видим, дисперсия оценки зависит только от расстояния между точкой х* и центром плана, т.е. полные и дробные двухуровневые факторные планы для линейных моделей вида (6.2) - ротатабелъные. Величина самой оценки выходной переменной у будет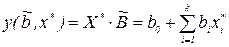 
Доверительный интервал для выходной переменной составляет: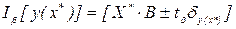 
, где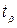 
берется из t-распределения при числе степеней свободы г = n0-1.
